Problem: Determine whether the following series converges.

Solution: The terms of this series are all positive, so we can use all those nice tests. But which of them will work? Since the terms feature factorials, the obvious choice is the Ratio test. But perhaps first it is a good idea to have a closer look at the terms to see how they behave (recall the definition of the double factorial in Functions - Theory - Elementary functions).

Since the last small fraction is about 1 for large k but it is always smaller than 1, it is not clear how the whole big fraction behaves, in particular whether it goes to 0. We try the Ratio test and see what happens, as usual we will put together parts with common origin.

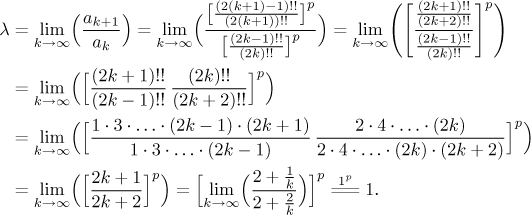
This is the indecisive value for the Root test and we do not know anything about the series yet.

What other options are there? We cannot integrate factorials, so the Integral test is out. Taking k-th root of factorials is also not wise and by the above result we know that we would get ϱ = 1, so there is no point in trying the Root test. There also seem to be no way to use comparison, so the traditional tests fail here.

If we want to succeed we have to reach deeper into our vaults, namely in the section More tests in Theory - Testing convergence we had some tests that refine the Ratio test, tests that can (sometimes) help when the Ratio test comes up inconclusive. We start with the simplest of them, the limit version of Raabe's test.

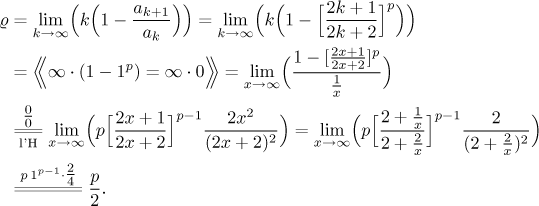
By the Raabe test, the given series converges if ϱ > 1, that is, if p > 2, and diverges if p < 2. By the way, this in particular means that the terms a_k go to zero for p > 2, in particular the expression inside (the ratio of factorials) goes to zero. Thus terms of the series go to zero for all positive p.

The case p = 2 remains undecided. One possibility is to use some more general version of Raabe's test. The general idea is to look at a_k+1/a_k − 1 and ask how much is 1/k present in this expression.

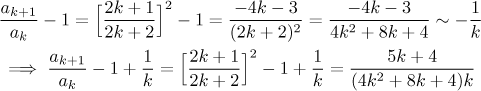
We see that 1/k is present 1-times, that is, A = 1 in those more general versions of Raabe's theorem, we therefore do not get convergence. However, to get divergence we need to do more work. We have two possibilities, since we have two more general versions of Raabe's test. We will try the one that we called the "most general".

Using the Limit comparison test we easily show that the series with terms v_k converges by comparing it to the p-series with p = 2.

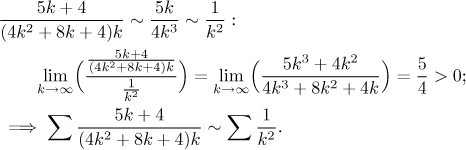
Thus we succeeded in setting up the "most general version" of Raabe's test, we have A = 1 and therefore the given series diverges for p = 2.

Conclusion: The given series converges exactly if p > 2.

Remark: While the first step was quite straightforward, deciding the p = 2 case took some effort. Is there an alternative? The Kummer test is supposed to be very powerful, but guessing the right p_k in it is highly non-trivial and way beyond the scope of Math Tutor. We also see no benefit in condensation. There is one more test in that section and it looks promising, since the Gauss test is to a great extend algorithmic. We will try it, you will see that we will in fact just redo the above work in a different setting.

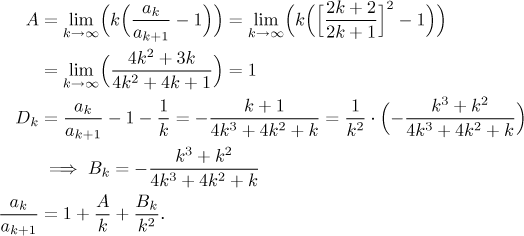
We succeeded to set up the situation as required in the Gauss test, note that B_k form a bounded sequence and r = 2 > 1. Thus Gauss's test applies and we can conclude that the given series diverges.

Next problem
Back to Solved Problems - Testing convergence