Problem: Determine whether the following series converges absolutely.

Solution: To determine whether the given series converges absolutely we will test whether the following series converges:

This is a series with non-negative terms and we have all the nice tests available. What tests will work? Since the series consists of powers (and roots), the best test for it is some comparison. We guess that for k large the "+1" part is negligible and can be ignored. One possibility is simple comparison by inequality.

The series on the right is divergent (by the p-test, p = 1/2 < 1), but our series is smaller and that is exactly the case when no conclusion is possible. So we try the Limit comparison test. First we confirm that the "+1" part can be ignored and then we make conclusions about similarity.

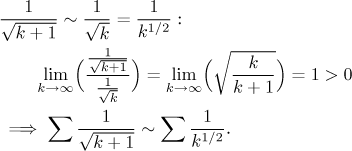
Now the divergence of the test series can be used to conclude that our series is divergent.

Conclusion: The given series is not absolutely convergent.

Is there another way to prove this divergence? We know that the Root test and the Ratio test do not work for series with polynomials (and roots). Indeed, we get the indecisive case 1.

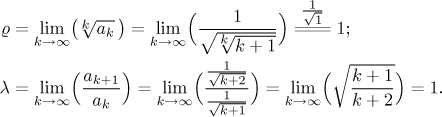
One last possibility: The terms of the series are given by the function f (x) = (x + 1)^−1/2 that is positive and decreasing, so we can apply the Integral test and pass from our series to the appropriate improper integral.

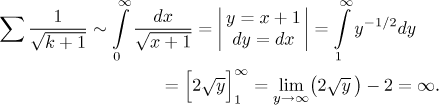
So the integral test confirms divergence of the series with absolute value.

Remark: The series itself is convergent. It is an alternating series and the terms b_k = (k + 1)^−1/2 are positive, decreasing and tend to 0, therefore the alternating series test confirms convergence of this series.

Next problem
Back to Solved Problems - Testing convergence