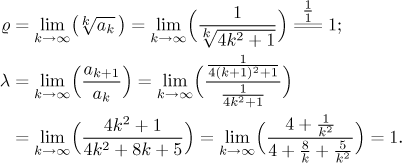Problem: Investigate convergence of the following series. (Does it converge? If it does, then how?)

Solution: First we address the question of convergence of the given series. What do we know about its terms? The numbers cos(kπ/2) attain values 1, 0, −1, 0, 1, 0,..., which means that the terms of the given series change signs, but they are not alternating. Thus we cannot directly use the Alternating series test. What else remains? There are two possibilities. One is to use the Dirichlet test. Indeed, the numbers a_k = cos(kπ/2) and b_k = 1/(k² + 1) satisfy its assumptions, in particular partial sums of the series

1 + 0 − 1 + 0 + 1 + 0 − 1 + ...

are only 0 and 1. This proves that the given series is convergent.

We could also use the Fact there which views the Dirichlet test as generalization of AST and applies to series with regular pattern of signs with sum of one period being zero - exactly our situation.

Is there a way to deduce this convergence without using advanced tests, just with the basic ones that every calculus student knows? Actually, there is. When we look at the given series carefully, we realize that it is in fact an alternating series, we just have to notice that all terms with k odd are zero, so we can drop them and reindex the series accordingly.

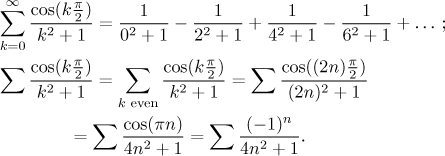
We see that the given series is indeed alternating, so applying the Alternating series test with b_k = 1/(4k² + 1) we conclude that the series is convergent.

Now we turn to the problem of absolute convergence. We want to investigate convergence of the series

The terms are all non-negative, but the cosine does not look too friendly. The absolute value rules out integration, so we get no help from the Integral test. Since the sequence |cos(kπ/2)| does not have a limit, we can expect trouble with all tests that use limit, so we do not feel like trying the Root test and the Ratio test either. We at last came to comparison tests, which is actually the natural approach here. Indeed, comparison is the recommended test for series with polynomials, moreover we have a natural upper bound for a part that we do not like here. We estimate:

We have a very nice comparison and the series on the right is known to be convergent, for instance by the p-test. Thus we conclude that the series on the left is also convergent.

Conclusion: The given series is absolutely convergent.

Remark: Since absolute convergence implies convergence, we could have saved some work if we started with absolute convergence right away.

Note that since the numerator with cosine does not have a limit, it makes no sense to claim that it looks like this or that for large k. Therefore there is no way we can use the Limit comparison test for this series. Thus we have an example of a series for which the plain Comparison test works but the limit version does not.

Remark: Note that if we use the alternative expression of the given series, then our situation when exploring absolute convergence becomes somewhat simpler.

Now we can use all tests, but only some of them yield anything. We know that for series with rational functions the best bet is comparison, usually its limit version. In this particular case both kinds of comparison are possible and lead to the correct answer.

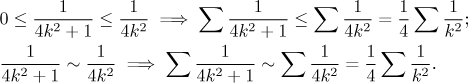
Since the function f (x) = 1/(4x² + 1) is positive, decreasing and relatively simple to integrate, also the Integral test is a viable option.

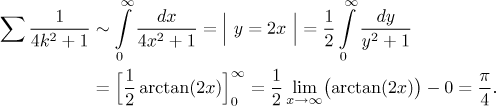
On the other hand, we know that series with rational functions cannot be handled using the Root test or the Ratio test, since there we get the indecisive case. Indeed,

Next problem
Back to Solved Problems - Testing convergence