We will prove here that for every x, the sum of
|sin(x)| and |sin(x + 1)|
is always at least sin(1). To this end, consider the function
f (x) = |sin(x)| + |sin(x + 1)|.
What are its extreme values? Since this function is π-periodic,
it is enough to
find its global extrema on [0,π].
We will apply the standard procedure using derivatives, see
Global extrema in
Derivatives - Methods Survey - Applications. However, in order to
differentiate we have to first get rid of the absolute value. Since we are
taking x between 0 and π,
the first absolute value can be simply ignored. However, the
second term can be both positive and negative and the critical value here is
π − 1. Thus we have two cases.
Case 1: x is between 0 and
π − 1. Then
f (x) = sin(x) + sin(x + 1).
f ′(x) = cos(x) + cos(x + 1).
When is the derivative equal to zero? We do not know how to solve this
equation analytically, but we can do it graphically. We look at the first
wave of cosine and start sliding a segment of length 1 along it, waiting for
the moment when the values at its ends will be exactly opposite.
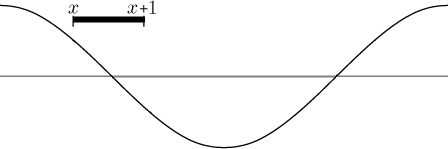
This happens when the segment is symmetric about the point
π/2, so
x = π/2 − 1/2. (The second such position is around the
point 3π/2,
but then x would be outside our range, that is, greater than
π − 1.)
To find global extrema over the interval
[0,π − 1] we check on endpoints and critical points:
• f (0) = sin(1);
• f (π/2 − 1/2) = sin(π/2 − 1/2) + sin(π/2 + 1/2) = 2sin(π/2 − 1/2);
• f (π − 1) = sin(π − 1) = sin(1).
Note that π/2 − 1/2 > 1 and
π/2 − 1/2 < π/2,
thus sine of it is greater than sin(1). Therefore the middle value is
maximum and minimum is sin(1) as claimed. On the first interval
it works.
Case 2: x is between
π − 1
and π. Then
f (x) = sin(x) − sin(x + 1).
f ′(x) = cos(x) − cos(x + 1).
When is the derivative equal to zero? Now we are waiting for
the moment when the values at the ends of the segment sliding over cosine will
be equal. There are two such positions, when the segment is over the origin
and when it is symmetric about the point
π. The first possibility yields
x = −1/2, which is outside our range, but the
other yields the relevant value
x = π − 1/2. To find global extrema over the interval
[π − 1,π] we
check on endpoints and critical points:
• f (π − 1) = sin(π − 1) = sin(1);
• f (π − 1/2) = sin(π − 1/2) − sin(π + 1/2) = 2sin(1/2);
• f (π) = −sin(π + 1) = sin(1);
Again, the middle value is maximum, one can see it for instance like this:
2sin(1/2) > 2sin(1/2)cos(1/2) = sin(2⋅1/2) = sin(1).
Again, we have minimum sin(1) as claimed. When we put the two cases together
we proved our claim.

