We will prove here that for every x, at least one of the numbers
|sin(x)|, |sin(x + 1)|, and
|sin(x + 2)| is greater than 1/2.
We will use a simple geometric argument, in particular we will use the fact
that π/6 is
slightly more than 1/2,
hence π/3 is
slightly more than 1; the value π/6 is obviously crucial here since sine is equal to
1/2 there.
We will do the proof by exploring all possible situations. If
|sin(x)| > 1/2 we are done. So assume that
this is not true. Then x must be between
nπ − π/6 and
nπ + π/6 for some integer n (see picture below).
If x were in the right half of this interval, then
x + 1 must be greater than
nπ + π/6
(since π/6 < 1) but smaller than
nπ + 5π/6, so
|sin(x + 1)| > 1/2 and we are done.
Thus the last case is when x is in the left half, that
is, between
nπ − π/6
and nπ.
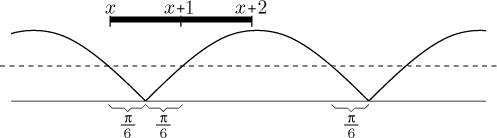
Then the number
x + 2 must again be greater than
nπ + π/6
(since π/3 < 2) but smaller than
nπ + 5π/6, so
|sin(x + 2)| > 1/2. Since this
was the last case left, we covered all possibilities and always found one
large value as needed.

