Definice.
Názvem mocninná řada se středem a rozumíme libovolnou řadu ve
tvaru
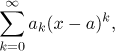
kde ak jsou reálná čísla.
Mocninné řady jsou přirozeným zobecněním Taylorových polynomů. Víme, že Taylorovy polynomy dávají (pokud máme štěstí) aproximaci funkcí, která se zlepšuje, když bereme delší polynomy, takže se dá čekat, že nekonečné polynomy dají přesně funkci, ze které vzešly. Než se k tomuto vztahu dostaneme, budeme zkoumat mocninné řady jako takové, jinými slovy se budeme snažit vyznat v "nekonečných polynomech"; mají zajímavé a užitečné vlastnosti.
Definice.
Názvem mocninná řada se středem a rozumíme libovolnou řadu ve tvaru
kde ak jsou reálná čísla.
Velice důležitým a užitečným pojmem jsou komplexní mocninné řady, což je mimo rozsah Math Tutoru; poznamenejme ale, že většina závěrů této sekce je pravdivá také v komplexním případě. Dokonce se občas na komplexní řadu odvoláme, protože některé pojmy jsou poněkud čitelnější ve více dimenzích.
Všimněte si, že obyčejný polynom může být také považován za mocninnou řadu.
Například polynom
Zpět k mocninným řadám. Základní pojem - obor konvergence - se pro mocninné řady chová velice pěkně. Zatímco u obecných řad funkcí může být obor konvergence dost podivný, zde víme najisto, že tato množina je nejlepší možná - interval (v komplexní rovině kruh, obecně koule). Začneme následujícím pozorováním.
Fakt.
Uvažujme mocninnou řadu se středem a. Pokud existuje takové x0, že daná řada v x0 konverguje, pak tato řada konverguje absolutně ve všech x splňujících
|x − a| < |x0 − a|.
To je zrovna případ, kdy mohou komplexní čísla (nebo body v rovině) pomoci v porozumění. Jestliže máme konvergenci v nějakém bodě x0, tak dostaneme absolutní konvergenci na vnitřku kruhu se středem a, na jehož obvodu x0 leží.
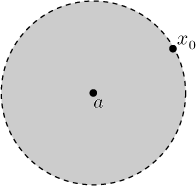
Řečeno jinak, tato řada nutně konverguje na okolí
Všimněte si, že každá řada konverguje ve svém středu a. Ten Fakt ukazuje, že jestliže se s konvergencí dokážeme posunout z a ven (směrem od středu), pak také automaticky rozšiřujeme absolutní konvergenci. Jsou tři možné situace. Jedna je, že kromě středu a žádná konvergence není. I to se může stát. Další situace je, že dokážeme "posunout" konvergenci libovolně daleko od a, pak také dostaneme absolutní konvergenci všude. Třetí možnost je, že konvergenci "rozšíříme" jak jen to je možné od a, ale nemůžeme jít libovolně daleko, existuje mez, za kterou se nedostaneme. Pak dostaneme okolí (v komplexním případě kruh, v reálném případě interval okolo a) takové, že řada konverguje absolutně uvnitř a diverguje venku (kdyby byl byť jediný bod konvergence venku, tak by šlo podle Faktu také příslušně rozšířit obor konvergence).
Máme tedy následující tvrzení.
Věta.
Uvažujme mocninnou řadu se středem a. Existuje čísloR ≥ 0 (včetněR = ∞ ) takové, že daná řada konverguje absolutně ve všech x splňujících|x − a| < R a diverguje ve všech x splňujících|x − a| > R .
Toto číslo se dá najít jako
Tyto vzorce také zahrnují případy
Definice.
Uvažujme mocninnou řadu se středem a. Číslo R z věty výše se nazývá poloměr konvergence této řady.
Tu větu (včetně vzorců) jsme dostali takto. Danou mocninnou řadu jsme
testovali na absolutní konvergenci pomocí vhodných kritérií a ukázalo se, že
konvergence záleží na vzdálenosti od středu
Příklad: Vyšetřete konvergenci řady
![]()
Použijeme
podílové kritérium
k vyšetření absolutní konvergence této řady.
Poznámka: K označení členů řady v podílovém kritériu použijeme
Ak, protože tradiční
ak je v kontextu mocninných řad použito pro
koeficienty, nikoliv pro celé členy řad.
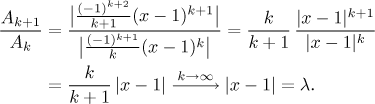
(Připomeňme, že v posledním kroku jsme dělali limitu vzhledem ke k,
x je zde nějaký pevně zvolený parametr.)
Test teď ukazuje, že zkoumaná řada konverguje absolutně, jestliže
Co můžeme říct o konvergenci v krajních bodech? To se musí zkoumat individuálně, všimněte si, že podílové kritérium dává pro x z hranice oboru konvergence lambda rovno 1, takže to nepomůže.
![]()
Toto je harmonická řada, o které víme, že diverguje.
![]()
Toto je alternující verze harmonické řady a podle Leibnizova kritéria konverguje, viz Konvergence obecných řad v části Teorie - Testování konvergence.
Závěr: Tato řada konverguje na oboru konvergence
Poznámka: Jak víme, že nemáme absolutní konvergenci v 2? Všimněte si,
že když vezmeme řadu získanou s
To znamená, že buď máme absolutní konvergenci v obou krajních bodech (pak tam také musíme mít konvergenci), nebo nemáme absolutní konvergenci v žádném. Z praktického pohledu to znamená, že pokud nemáme v obou krajních bodech konvergenci, tak krajní body automaticky nezahrnujeme do oboru absolutní konvergence. Ještě se k tomu vrátíme níže.
Příklad: Vyšetřete konvergenci řady
![]()
Použijeme podílové kritérium k vyšetření absolutní konvergence této řady.
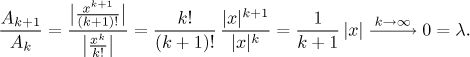
Test říká, že zkoumaná řada konverguje absolutně, jestliže je lambda méně než
1, ale vidíme, že toto se stane vždy, bez ohledu na x. Máme tedy
Příklad: Vyšetřete konvergenci řady
![]()
Použijeme odmocninové kritérium k vyšetření absolutní konvergence této řady.
![]()
Test říká, že zkoumaná řada konverguje absolutně, jestliže ró je menší než
1, ale vidíme, že to se stane jen pro
Poznámka: Daná řada nesplňuje definici mocninné řady, ale dá se na ni přepsat.
![]()
Teď vidíme, že střed je opravdu
Vidíme, že ty tři případy diskutované výše (R kladné,
Připomeňme Fakt výše, který v zásadě říká, že když máme v nějakém bodě konvergenci, tak už získáme konvergenci všude vevnitř kruhu až po tento bod (viz ten obrázek výše pro komplexní případ, je dost názorný). Pomocí tohoto jsme pak usoudili, že obor konvergence má tvar disku. Předpokládejme teď, že máme řadu s kladným (tedy i konečným) poloměrem konvergence. Pak nám ten Fakt (nebo Věta o poloměru konvergence) nedovolují říct nic o konvergenci na obvodu disku konvergence. A je k tomu dobrý důvod, v typickém případě máme někde na obvodu konvergenci a jinde divergenci, občas je to divergence všude nebo konvergence všude. Ukážeme teď, že onen diskutovaný Fakt lze zesílit, jestliže je konvergence v onom speciálním bodě "lepší".
Fakt.
Uvažujme mocninnou řadu se středem a. Pokud existuje takové x0, že daná řada v x0 konverguje absolutně, pak tato řada konverguje absolutně ve všech x splňujících
|x − a| ≤ |x0 − a|.
Vyplývá z toho, že jestliže máme dokonce absolutní konvergenci v nějakém bodě obvodu kruhu konvergence, pak už máme konvergenci na celém obvodu.
Algebraické operace s řadami jsou definovány přirozeným způsobem, pomocí definice pro číselné řady, vzhledem k jejich tvaru je ale možné spojovat jen řady se stejným středem. Důležitý fakt je, že sčítání/násobení mocninných řad nezkazí konvergenci (pro Cauchyho součin to plyne z absolutní konvergence, kterou pro mocninné řady máme automaticky). Navíc jsou součty takových řad přesně tím, čím by měly být.
Věta.
Uvažujme mocninné řady
s poloměry konvergence po řadě
R f aRg. Pak platí následující.(i) Součet těchto řad konverguje s poloměrem konvergence
R ≥ min(R f ,Rg) a
(ii) Pro reálné číslo c platí, že c-násobek řady konverguje se stejným poloměrem konvergence a
(iii) Cauchyho součin těchto řad konverguje s poloměrem konvergence
R ≥ min(R f ,Rg) a
Poznamenejme, že pokud jsou v části (i) poloměry Rf a Rg různé, pak se už R nutně rovná jejich minimu, viz tento příklad v části Řešené příklady - Řady funkcí. Vzorec pro Cauchyho součin je zcela přirozený, stačí si jej napst v dlouhém tvaru a je to jasné, pro jednoduchost použijeme střed 0.
Tato věta má jednu zajímavou interpretaci. Zvolme pevně jeden střed
a, uvažujme množinu S všech posloupností
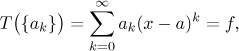
pak je toto zobrazení lineární. Jinými slovy, namísto funkcí (které jsou někdy trochu příliš komplikované, aby se s nimi dobře pracovalo), můžeme pracovat s posloupnostmi, které je reprezentují, a tato korespondence je nejlepší možná, zahrnuje i obvyklé lineární operace. Z algebraického pohledu jsou tedy oba prostory stejné. (Zde také potřebujeme vědět, že toto zobrazení je prosté, což je pravda díky výsledku o jednoznačnosti níže.)
Jak do toho zapadá to třetí tvrzení? Jestliže je funkce f zakódována
posloupností
Větu můžeme symbolicky vyjádřit takto: Pokud zavedeme přiřazení
Dají se také vyrobit vzorce pro další věci, které s funkcemi děláme, například pro substituci (mimochodem, dělení je popravdě řečeno dost drsné), ale to už je více svázáno s rozvojem funkcí, který probíráme v následující sekci.
Důležitým faktorem při práci s řadami funkcí je otázka stejnoměrné konvergence. Zde je situace asi nejlepší možná. Stačí se vyhnout hranici a jsme v pohodě.
Věta.
Uvažujme mocninnou řadu se středem a a poloměrem konvergenceR > 0. Pak pro každé kladnér < R tato řada konverguje stejnoměrně na⟨a − r,a + r⟩.
Obecněji, taková mocninná řada konverguje stejnoměrně na libovolném
uzavřeném intervalu, který je podmnožinou
Jako obvykle, pokud použijeme jazyka okolí: "Mocninná řada konverguje stejnoměrně na libovolném uzavřeném okolí, které je obsaženo v oboru konvergence," dostaneme tvrzení, které platí také v jiných situacích (komplexní řady atd.).
Tato věta je dokonce ještě lepší, než se zdá na první pohled. Všimněte si,
že dostáváme stejnoměrnou konvergenci tak blízko k hranici, jak jen chceme.
Pokud si vezmeme libovolné x0 z
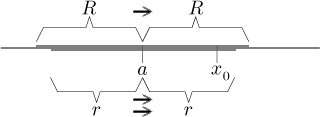
Krátce řečeno, dostáváme stejnoměrnou konvergenci okolo všech bodů uvnitř oboru konvergence, takže můžeme použít všechny ty pěkné vlastnosti, které jsme pro stejnoměrnou konvergenci měli (viz Řady funkcí) všude v oboru konvergence. Dostáváme tedy následující velice užitečné tvrzení.
Věta.
Uvažujme mocninnou řadu se středem a a poloměrem konvergenceR > 0. Nechť f je funkce, kterou tato řada definuje na svém obor konvergence.
(i) Funkce f je spojitá naUR(a) = (a − R,a + R).
(ii) Funkce f je diferencovatelná naUR(a) = (a − R,a + R), na této množině
a konvergence této řady je stejnoměrná na
⟨a − r,a + r⟩ pro libovolné kladné r < R.
(iii) Funkce f je integrovatelná naUR(a) = (a − R,a + R), na této množině má primitivní funkci
a konvergence této řady je stejnoměrná na
⟨a − r,a + r⟩ pro libovolné kladné r < R.
Dá se to také říct takto. Je-li dána mocninná řada, můžeme ji derivovat člen po členu a poloměr konvergence se nezmění, konvergence zůstane pěkná a výsledek je logický: Když derivujeme člen po členu, dostaneme totéž, jako bychom derivovali funkci, která je řadou definována (odpovídající tvrzení platí i pro integrování). Fakt, že můžeme mocninné řady snadno a spolehlivě derivovat a integrovat, je jedním z hlavních důvodů pro jejich užitečnost a popularitu.
Všimněte si dvou věcí. Za prvé, v posledním výrazu napravo v (ii) jsme
vynechali první člen v indexaci. Není to nutné, protože když je
Za druhé, řady, kterou dostaneme po derivování a integrování, nejsou ve správném tvaru, na to je třeba udělat ještě posun v indexu.
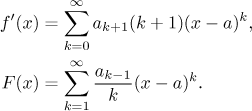
Zase záleží na situaci, někdy se to dělá (například jestli chcete prezentovat výsledek v pěkném tvaru), ale v praxi to lidem většinou nestojí za to.
Poznámka: Ta věta nám umožňuje derivovat a integrovat řadu pouze
uvnitř jejich oborů konvergence - a z dobrého důvodu. Jestliže mocninná řada
také konverguje v nějakém krajním bodě svého oboru konvergence, pak tato
konvergence nemusí přežít derivování či integrování. Jako ukázku se
podívejte na
první příklad výše, o té řadě jsme
zjistili, že konverguje na intervalu
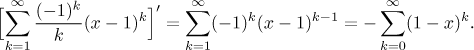
Je snadné ověřit, že tato řada už v bodě 2 nekonverguje.
Iterací věty zjistíme, že mocninné řady dávají funkce, které mají derivace všech řádů.
Důsledek.
Uvažujme mocninnou řadu se středem a a poloměrem konvergenceR > 0. Nechť f je funkce, kterou řada definuje na svém oboru konvergence. Pak pro každé přirozené číslo n má funkce f svoun-tou derivaci naUR(a), na této množině
a konvergence této řady je stejnoměrná na
Ur(a) pro libovolné kladnér < R.
Teď si představme, že máme dvě řady se středem a, které konvergují a
jejichž součty jsou si rovny na nějakém okolí bodu a. Napíšeme tuto
rovnost řad a pak zderivujeme n krát na obou stranách, dostaneme
nalevo a napravo výrazy jako v Důsledku. Když do této rovnice dosadíme
Důsledek (jednoznačnost).
Uvažujme dvě mocninné řady se středem a, řadu∑ ak(x − a)k a řadu∑ bk(x − a)k takové, že obě konvergují na nějakémUr(a) pro kladný poloměr r.
Jestliže se na tomto okolí rovnají součty obou řad, pak jsou řady nutně stejné, tedyak = bk pro všechna k.
To mimo jiné znamená, že řada je jednoznačně dána svými hodnotami na nějakém okolí bodu a, třeba i velmi malém. Jakmile známe její hodnoty na nějakém malinkém okolí a, pak už jsou určeny i hodnoty v dalších bodech konvergence, dokonce i když řada konverguje všude.
To také znamená, že když máme polynom, tak jej není možné zapsat jinak, ani jako skutečně nekonečnou mocninnou řadu (se stejným středem, samozřejmě; při jiné volbě středu získáme jiné vyjádření pro tutéž funkci).
Poznámka o krajních bodech: Už jsme poznamenali, že konvergence řady v krajních bodech nemusí přežít derivování, takže jsme nemohli udělat nějaké obecné tvrzení v druhé a třetí části věty výše. To první tvrzení (o spojitosti) ale není nejlepší možné. Dá se vylepšit, což už nedostaneme automaticky ze stejnoměrné konvergence, ale máme na to speciální větu.
Věta (Abelova věta o konvergenci).
Uvažujme mocninnou řadu se středem a a poloměrem konvergenceR > 0. Nechť je f funkce, kterou tato řada definuje na svém oboru konvergence.
• Jestliže řada konverguje va + R, pak je tam f spojitá zleva a řada konverguje stejnoměrně také na intervalu⟨a,a + R⟩.
• Jestliže řada konverguje va − R, pak je tam f spojitá zprava a řada konverguje stejnoměrně také na intervalu⟨a − R,a⟩.
Dá se to shrnout takto.
Předpokládejme, že mocninná řada se středem a a poloměrem konvergence
R > 0 konverguje na intervalu I (takže interval I určitě obsahuje(a − R,a + R), ale také může obsahovat jeden či oba krajní body). Pak je výsledná funkce f spojitá na I a konvergence této řady je stejnoměrná na libovolném uzavřeném intervalu J, který je podmnožinou I.
Takže pokud je I uzavřený, čili pokud daná řada konverguje na