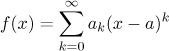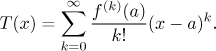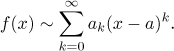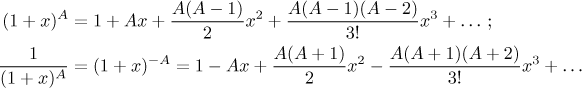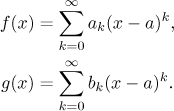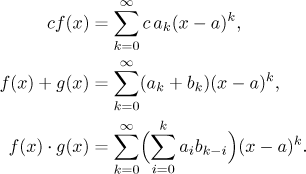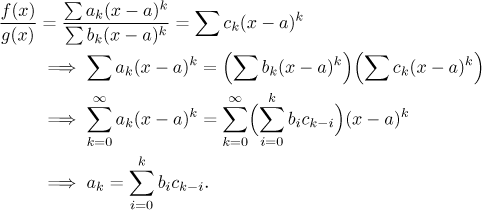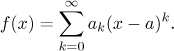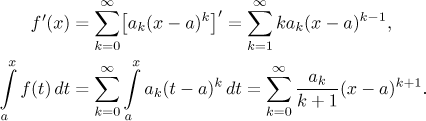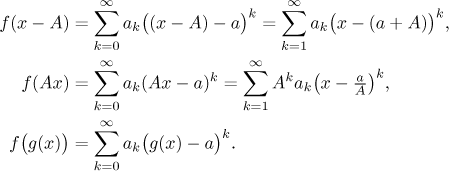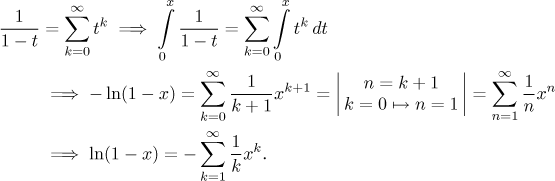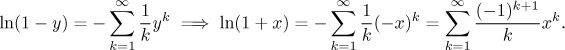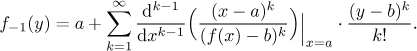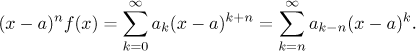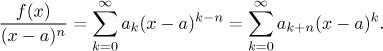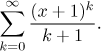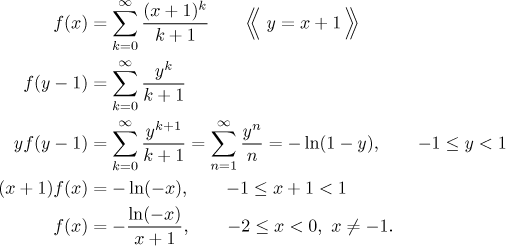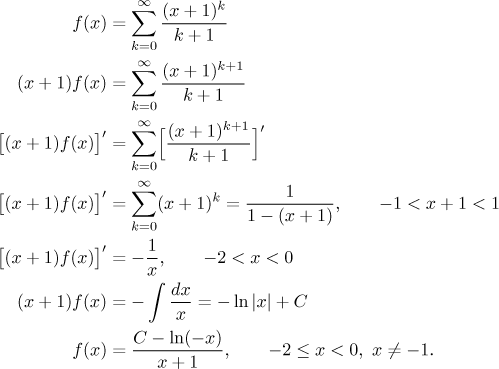Taylorovy řady, rozvoj funkcí, sčítání řad
Zde se podíváme na hlavní otázku. Máme funkci f a číslo a a
rádi bychom tuto funkci vyjídřili jako součet mocninné řady se středem
a. Začneme teorií a pak se podíváme na rozvoj pomocí
vlastností. Na závěr se podíváme na opačný
proces, k dané řadě zkusíme najít její
součet.
Jak už jsme pro obecný případ naznačili v sekci
Systémy funkcí, jsou dvě otázky,
které musíme zodpovědět: Které funkce lze takto vyjádřit a jak pro ně
najdeme jejich řadu. První otázka je opravdu těžká, za chvíli dáme jen
částečnou odpověď. Začneme definicí.
Definice.
Nechť f je funkce a a nějaký bod z vnitřku jejího
definičního oboru.
Řekneme, že jsme funkci f rozvinuli v mocninnou řadu (v
a), jestliže najdeme nějakou mocninnou řadu takovou, že
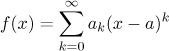
na nějakém okolí a.
Této mocninné řadě se pak říká rozvoj funkce f.
Z výsledků
předchozí sekce vyplývá, že
každá funkce, kterou lze takto rozvést, musí mít derivace všech řádů v
a. To nám říká, že nemá smysl se pokoušet rozvíjet jiné funkce. Také
to říká, že když mluvíme o rozvoji, máme všechny ty derivace k dispozici.
Počátečním bodem našeho zkoumání je Důsledek na konci
předchozí sekce.
Předpokládejme, že máme funkci, kterou lze vyjárdřit jako řadu v a.
Jestliže dosadíme tento střed a do vzorce pro n-tou derivaci,
okamžitě dostáváme následující.
Věta (jednoznačnost rozvoje).
Nechť f je funkce, kterou lze rozvinout v mocninnou řadu
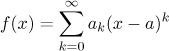
na nějakém okolí bodu a. Pak pro každé k koeficient
ak nutně splňuje
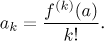
Jinými slovy, existuje jen jeden způsob, jak rozvinout funkci v mocninnou
řadu (pokud je to vůbec možné). Tato jedinečná řada si zasluhuje jméno.
Definice.
Nechť f je funkce a a nějaký bod z vnitřku jeho
definičního oboru. Předpokládejme, že f má derivace všech řádů v
a. Pak definujeme její Taylorovu řadu v a vzorcem
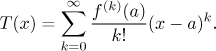
Vzoreček pro koeficienty je stejný jako v případě
Taylorova polynomu,
takže je to opravdu něco jako "nekonečný Taylorův polynom".
Všimněte si, že ta věta výše byla jen implikace. To znamená, že jakmile
funkci rozvineme v mocninnou řadu, pak už ta řada musí nutně být Taylorovou
řadou. Když ale vezmeme funkci se všemi derivacemi v a a vytvoříme
Taylorovu řadu podle příslušného vzorce, tak už není zaručeno, že ta řada
bude konvergovat někde jinde než v a, a i kdyby konvergovala, tak
není jisté, zda bude konvergovat k původní funkci f.
Například v
této poznámce ukazujeme příklad
funkce, která je "pěkná" podle většiny měřítek (má derivace všech řádů a
všude), její Taylorova řada konverguje ke svému součtu stejnoměrně na celé
reálné ose, ale přesto je součet této Taylorovy řady roven původní funkci
jen v jednom bodě, ve středu řady (kde musí být rovnost pro všechny funkce a
řady, takže nebylo na výběr). Situace, kdy máme problém přinutit řadu, aby
šla na správné místo, se objevuje při práci se systémy funkcí často a
přivádí nás k následujícímu značení.
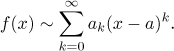
Tilda znamená, že řada napravo byla získána z f pomocí vzorců výše
(je to Taylorova řada pro f ), ale také to znamená, že tento
proces vytváření řady byl čistě formální, v této chvíli nemáme žádné
informace o tom, zda součet této řady má něco společného s f.
Naším cílem je samozřejmě změnit tuto tildu v rovnost, čili rádi bychom
viděli, že Taylorova řada napravo konverguje k f alespoň někde (kromě
a, kde je konvergence automatická). Jak se to dá poznat? Podle
definice bychom měli vzít částečné součty TN řady
T a podívat se, zda konvergují k f.
Ekvivalentně řečeno, rádi bychom zjistili, jak se chovají rozdíly
| f − TN|,
přitom doufáme, že půjdou k nule pro N jdoucí do nekonečna. Něco
takového už jsme ale viděli, protože TN je přesně
Taylorův polynom
(viz Derivace - Teorie - Aplikace), takže o tom rozdílu toho docela dost
víme. Například pro něj máme
Lagrangeův
odhad. Můžeme tedy otázku přeformulovat následovně:
Předpokládejme, že f má derivace všech řádů na nějakém okolí
U bodu a. Nechť je x takové, že uzavřený interval I
s krajními body a a x leží v U. Chceme vědět, kdy je
pravda, že
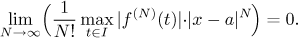
Všimněte si, že v tomto vzorci je x pevně zvoleno a proto je
x − a konstanta. Když si připomeneme,
že
cN/N! jde v nekonečnu k nule,
tak vidíme, že všechno závisí na tom, jak rychle to maximum roste vzhledem k
N. Pokud neroste vůbec nebo roste velice pomalu, pak jde Lagrangeův
odhad chyby k nule. Dostaneme tedy následující.
Věta.
Nechť f je funkce taková, že má derivac všech řádů na nějakém
okolí U bodu a. Nechť T je její Taylororova
řada v a.
Jestliže existuje konstanta M taková, že
| f (k)(t)| ≤ Mk
pro všechna přirozená čísla k a všecha t z U, pak T
konverguje (stejnoměrně) k f na U.
Dostáváme tedy skupinu funkcí, jejichž Taylorova řada je jim opravdu rovna,
jmenovitě funkce se stejnoměrně omezenými derivacemi. Tato podmínka je
nicméně příliš omezující, jsou také další funkce, jejichž Taylorova řada
konverguje, kam má. Najít správnou charakterizaci je velice těžké, rozhodně
za obzorem Math Tutoru, a necháme to profesionálním matematikům.
Jsou funkce, jejichž rozvoje najdeme velice snadno. Podle jednoznačnosti
rozvoje jsou mocninné řady sami sobě Taylorovými řadami (se stejným
středem). Rozvinout je s jiným středem než "vlastním" už tak snadné není,
ale pořád to jde v případě řad "konečných", tedy polynomů. Tam jen stačí
vytvořit správný střed. Pokud chceme například najít Taylorovu řadu pro
x2 se středem a = 1, tak
prostě uděláme
x2 = [(x − 1) + 1]2 = (x − 1)2 + 2(x − 1) + 1.
Ten poslední vzorec dává mocninnou řadu se středem 1 (její koeficienty jsou
nulové pro k > 2) a tudíž je to ona žádaná
Taylorova řada. (Samozřejmě bychom dostali stejnou řadu, pokud bychom
použili vzorec z definice.) U řad nekonečných už bychom s takovými úpravami
měli dost problém.
Teď se podíváme na šest slavných rozvojů, které jsou základem pro většinu
dalších.
Věta.
Následující rozvoje platí na vyznačených množinách.

Jak tyto vzorce naznačují, volba
a = 0
pro střed je velice populární. Je dokonce tak populární, že pro Taylorovy
řady s tímto středem někteří lidé používají tradiční název
McLaurinova řada. Není to ale univerzální a najde se to především ve
starších textech.
Ve všech šesti případech se najde vzorec pro Taylorův polynom snadno z
definice. Jak je to s jejich konvergencí? Druhý a třetí vzoreček je jasný,
konvergence plyne s předchozí věty (sinus a kosinus mají všechny derivace
všude omezené jedničkou).
Větu můžeme použít i pro exponenciálu, ale už ne globálně, protože
exponenciála je omezená jen na omezených množinách. To ale není problém.
Pokud si vezmeme libovolné reálné číslo x, tak můžeme uvažovat
například otevřené okolí
U2|x|(0). To je omezená množina a
všechny derivace funkce ex jsou tam tedy stejnoměrně
omezené, takže podle předchozí věty tam příslušná Taylorova řada konverguje
k exponenciále; konverguje tedy k exponenciále také v x, protože
x náleží do tohoto okolí. Pro úplnost ukážeme také přímý důkaz pomocí
Lagrangeova odhadu, viz
tato poznámka.
Rozvoj logaritmu lze získat více způsoby, vrátíme se k tomu také ještě
níže; co se týče konvergence, zmíněný interval je evidentně největší, v jaký
můžeme doufat, protože jsme v
předchozí sekci dokázali, že je
to přesně obor konvergence této Taylorovy řady. Zbývá ukázat, že součet řady
na tomto oboru je přesně ln(x). Zde už ale nemůžeme použít předchozí
větu, protože derivace nejsou stejnoměrně omezené. Tento případ je proto
komplikovanější, pro detaily viz
tato poznámka.
Pátý vzorec je prostě jen
geometrická řada, takže na
tom není nic nového.
Asi nejzajímavější z těch šesti je poslední vzorec, zvaný také
binomická řada nebo binomický rozvoj. Platí pro všechna
c a A, což mimo jiné znamená,že kombinační čísla lze také
definovat pro obecné číslo A. Dělá se to podle toho druhého vzorce s
tím, že když
k = 0, tak dostaneme 1. Jako příklad si ukážeme, jak taková
řada vypadá pro c = 1, což se používá často. Ukážeme si
také speciální vzorec pro "mínus A", který je občas užitečný při
práci z převrácenou hodnotou. Oba vzorce fungují pro
|x| < 1.
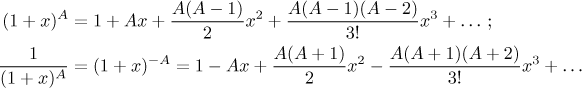
Všimněte si také, že když je A přirozené číslo, tak podle
definice jsou všechny koeficienty pro
k > A nulové. Suma je tedy konečná,
vždy konverguje a je to ten povědomý binomický vzorec, který známe ze
střední.
Tyto vzorce jsou důležité třeba proto, že jen zřídka rozvíjíme funkce podle
definice, jako jsme to dělali výše. Ve většině případů používáme různé
triky, abychom získali ze známých rozvojů nové. Těch šest nahoře jsou
východisky pro většinu takových výpočtů. Co se týče triků, teď se k nim
dostaneme.
Rozvoj a operace
Abychom získali rozvoje nových funkcí ze známých rozvojů, používáme
vlastnosti, které máme potvrzeny pro řady. Věta o
algebraických operacích z
předchozí sekce dává následující užitečný fakt.
Věta.
Předpokládejme, že máme následující rozvoje na nějakém okolí bodu a.
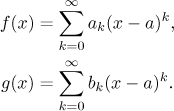
Pak na tomto okolí také máme
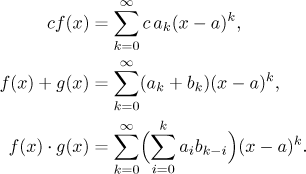
Jak je to s dělením f /g? Evidentně stačí
vědět, jak rozvinout funkci 1/f (za předpokladu, že
f (a) ≠ 0).
Věta.
Předpokládejme, že funkci f můžeme rozvinou v Taylorovu řadu v
a a že
f (a) ≠ 0. Pak lze také funkci
1/f rozvinout v Taylorovu řadu v a a
tato řada má kladný poloměr convergence.
Tato věta nenabízí žádný vzorec pro onu novou řadu - a z dobrého důvodu,
nedá se totiž žádným rozumným způsobem popsat. V praxi se používá
metoda neurčitých koeficientů. Dá se vlastně přímo aplikovat na
f /g a vzít 1/f jako
speciální případ. Předpokládejme, že jak f tak g jsou
rozvinuty ve své Taylorovy řady v a a že
g(a) ≠ 0. Podle naší věty lze pak
rozvinout i podíl v Taylorovu řadu se zatím neznámýmí koeficienty
ck.
Můžeme psát
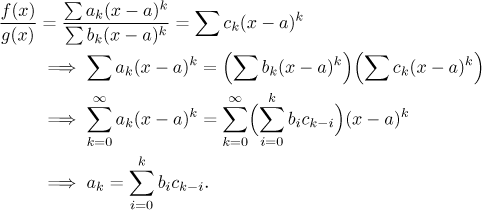
Výsledný systém nekonečně mnoha lineárních rovnic o nekonečně mnoha
neznámých
ck se obvykle nedá řešit explicitně,
ale dovolí nám vypočítat tolik koeficientů
ck, kolik chceme, což je velmi
užitečné, když chceme aproximovat
f /g
pomocí konečné části Taylorovy řady. Pro příklad odkazujeme na Řešené
příklady, jmenovitě
tento příklad (je nezvykle
pěkný, ale myšlenku ukazuje dobře) a
tento příklad
(ten už je typičtější).
Často také nacházíme vztah mezi funkcemi pomocí derivace a integrálu. Pak
použijeme
tuto větu z předchozí sekce.
Věta.
Předpokládejme, že máme následující rozvoj na nějakém okolí bodu
a.
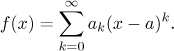
Pak na tomto okolí také
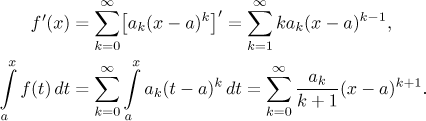
V druhém tvrzení se také dá použít neurčitý integrál, ale pak je třeba najít
správnou konstantu. Ukážeme na to jeden příklad níže. Jsou ale i další
operace, které mohou pomoci při rozvoji nových funkcí.
Věta (substituce v řadě).
Předpokládejme, že máme následující rozvoj na nějakém okolí bodu
a.
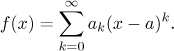
Pak také
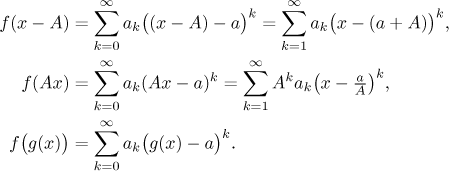
První tvrzení platí pro libovolné A a poloměr konvergence nové řady
je stejný jako původní, ale její střed (a obor konvergence) se příslušným způsobem
posunou.
Druhé tvrzení platí pro všechna nenulová A a poloměr konvergence nové
řady je
Rf /|A|.
Třetí tvrzení je trochu problematické, protože výsledek je mocninná řada jen
pro velmi speciální g. Obor konvergence se pak musí řešit
individuálně.
U prvních dvou tvrzení můžeme dokonce i specifikovat obor konvergence nové
řady. V prvním tvrzení je nový obor stejný jako ten původní, jen posunutý. V
druhém případě se nový obor konvergence dostane smrsknutím původního, pro
záporná A se také musí otočit kolem a. Jinými slovy, pokud
původní řada konverguje v pravém krajním bodě, tak nová také konverguje v
pravém krajním bodě pro A > 0 a konverguje
v levém krajním bodě pro A < 0. Je to
všechno jen selský rozum a dobré pochopení substituce.
Příklad: Teď odvodíme rozvoj pro
f (x) = ln(1 − x) v
a = 0.
Klíčem k tomuto rozvoji je pozorování, že
f ′(x) = −1/(1 − x)
a to je přesně součet
geometrické řady,
kterou všichni známe. Takže začneme se vzorcem pro geometrickou řadu
(použijeme proměnnou t) a pak budeme integrovat obě strany od 0 do
x
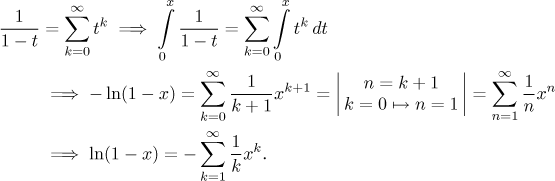
Tato řada se pro logaritmus používá často. Původní řada konverguje pro
t splňující −1 < t < 1,
takže ta nová také konverguje alespoň na této množině a její poloměr
konvergence musí zůstat stejný (tj. 1). Mohli jsme ale získat konvergenci v
některém krajním bodě. Když dosadíme
x = −1
a
x = 1
a použijeme vhodné testy, tak zjistíme, že obor konvergence této řady je
⟨−1,1).
Jak víme, že součet této řady v
x = −1
je roven
ln(2)?
Jedna možnost je použít spojitost, viz
Abelova věta o konvergenci
v předchozí sekci. Máme tedy rozvoj platný na
⟨−1,1).
Pokud tento výsledek zapíšeme pomocí y a pak použijeme substituci
y = −x,
dostaneme
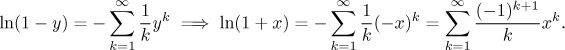
Původní řada konverguje pro y splňující
−1 ≤ y < 1,
takže když za y dosadíme
-x, dostaneme pro novou řadu obor konvergence
(−1,1⟩.
Na druhou stranu, pokud dosadíme
y = 1 − x,
pak dostaneme přesně tu řadu pro ln(x),
kterou jsme měli v oné
Větě o rozkladech.
Vzhledem k potížím, které jsme měli s nalezením řady pro
1/f, je možná překvapující, že existuje explicitní
způsob rozvoje inverzní funkce.
Věta (Lagrangeův inverzní vzorec).
Předpokládejme, že funkci f lze rozvinout v řadu na nějakém okolí
bodu a. Předpokládejme dále, že f ′(a)
není nula. Označme
b = f (a).
Pak existuje okolí bodu a, na kterém je funkce f invertibilní,
a okolí bodu b, na kterém lze tuto inverzní funkci
f−1 rozvinout v mocninnou řadu. Navíc lze
tuto řadu najít jako
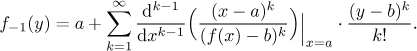
Tuto část uzavřeme ještě jedním užitečným tvrzením.
Věta.
Předpokládejme, že máme následující rozvoj na nějakém okolí bodu
a.
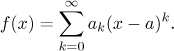
Pak na tomto okolí také máme následující rozvoje.
(i) Pro každé přirozené číslo n,
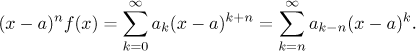
(ii) Jestliže má f kořen násobnosti n v a, pak
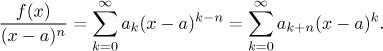
Druhé tvrzení má smysl z následujícího důvodu. Jestliže je a kořenem
násobnosti n pro f, pak je prvních
n − 1 derivací f v a nula
(viz tato poznámka).
Proto je také prvních n − 1 koeficientů Taylorovy
řady rovno nule, což znamená, že ve skutečnosti v řadě pro f indexy
začínají v n, ne v 0. To vysvětluje, proč po posunu indexu dostaneme
druhý vzorec.
Pro další příklady na použití výše popsaných vlastností k rozvoji funkcí viz
Přehled metod
a
Řešené příklady - Řady funkcí.
Část o vlastnostech Taylorových řad uzavřeme jedním snadným faktem, který
už se dal uhodnout z oné šestice rozvojů výše.
Fakt.
Nechť je f funkce, která má Taylorovu řadu se středem v
a = 0, nechť jsou ak
její koeficienty.
Jestliže je f lichá, pak
ak = 0 pro všechna sudá k.
Jestliže je f sudá, pak
ak = 0 pro všechna lichá k.
Sčítání řad
Už jsme několikrát zmínili, že sčítání řada bývá dosti obtížné. Výše popsané
triky pro rozvoj funkce lze také použít k sečtení dané mocninné řady (za
předpokladu, že máme štěstí). Základní myšlenka je, že změníme danou řadu v
jinou, kterou už známe, pomocí transformací z probraných vět, přičemž si
hlídáme, co to dělá s jejím součtem. Nejlépe se to vysvětlí na příkladě.
Příklad: Najděte součet řady
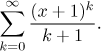
Existuje řada, která takto vypadá? Je řada, která má členy
yk/k,
a my se dokážeme dostat téměř k ní tak, že označíme
y = x + 1.
Zbývá upravit mocninu tak, aby souhlasila s číslem ve jmenovateli, ale to
není problém. Jdeme na to.
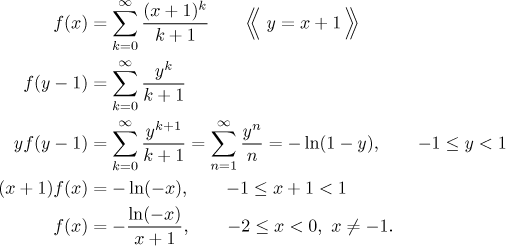
Jak je to s hodnotou x = −1? To je snadné,
prostě ji dáme do dané řady a zjistíme, že
f (−1) = 0.
Můžeme také zkusit jiný přístup. Často se potřebujeme zbavit k, které
je v řadě navíc. V naší řadě máme přebytečné
k + 1 ve jmenovateli, takže bychom ocenili,
pokud by se k + 1 objevilo i v čitateli.
Existuje způsob, jak dostat k do čitatele, jmenovitě zderivováním
řady. My potřebujeme k + 1, takže před
derivováním si tam potřebujeme vyrobit
(x + 1)k + 1.
Jakmile se zbavíme dělení členem k + 1,
použijeme
geometrickou řadu.
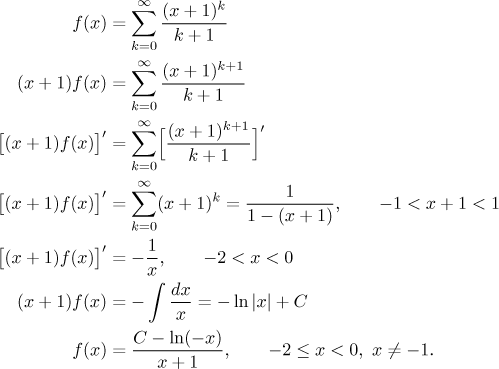
Zbývá upřesnit to správné C. Nejsnadnější způsob je prostě dosadit
nějaké pěkné x do poslední rovnosti. Protože nalevo dosazujeme do
f neboli do dané
řady, nemáme moc na výběr. Jediná hodnota, kterou do řady můžeme dát, je
x = −1, ale bohužel to je právě hodnota,
kterou v posledním řádku dosadit nemůžeme. Co se dá udělat?
Zdálo by se, že to můžeme vyřešit tím, že dosadíme do předposledního řádku.
Při bližším pohledu to ale není pravda. Všimněte si, že když
x = −1, pak na druhém řádku násobíme nulou,
což není v rovnicích dovoleno. Pro tuto hodnotu jsou tedy všechny
následující rovnosti podezřelé. Naštěstí pro nás se můžeme podívat ještě
blíže. Co to na předposledním řádku máme? Jednu funkci nalevo a druhou
napravo a jsme si jisti, že se rovnají pro všechna x z určitého
intervalu s výjimkou jednoho bodu přesně uprostřed. Protože jsou tyto dvě
funkce spojité, musíme pak mít rovnost i v tomto jednom bodě. Jsme
zachráněni, dosadíme −1 do předposledního řádku a zjistíme, že
C = 0. Protože jsme použili integraci, která
ovlivňuje krajní body, měli bychom se teď ještě podívat na konvergenci v −2
a v 0 a dostali bychom stejný závěr jako předtím.
Fourierovy řady
Zpět na Teorie - Řady funkcí