Rozvoj v mocninnou řadu (Taylorovu řadu): Přehled metod

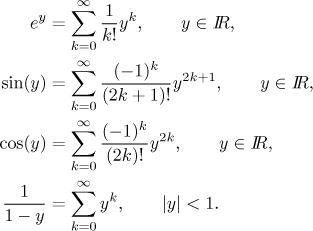
Je dána funkce f a střed a, chceme f rozvinout v mocninnou řadu s tímto středem.

Děláme to aplikováním rozličných transformací na řady, které už známe. Ve většině případů vystačíme s řadami pro exponenciálu, sinus, kosinus a geometrickou řadu, takže byste se je měli naučit.

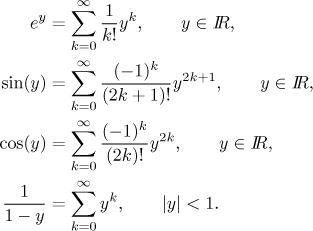
Někdy také přijdou vhod binomická řada a snad i některá verze řady pro logaritmus.

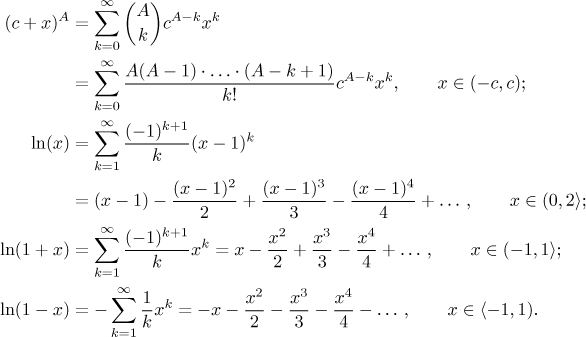
Základním nástrojem je substituce.

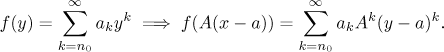
To se používá dost často, proto jsme také použili y v těch rozvojích výše. Platnost nového rozvoje se snadno určí tak, že se odpovídající omezení o y aplikuje na dosazovaný výraz A⋅(x − a) (viz Příklad níže).

Další populární modifikací rozvojů výše je násobení nějakou mocninou členu (x − a), někdy lze takovou mocninou i dělit (viz Taylorovy řady v části Teorie - Řady funkcí). Je také dobré si uvědomit, že pro polynomy je vytvoření řady triviální. To znamená, že když se rozhodujeme, se kterou řadou by měl náš rozvoj začít, tak můžeme ignorovat části daného výrazu, které nebudou zlobit, jmenovitě násobení polynomy a přičítání polynomů.

Je evidentní, že když chceme dostat mocninnou řadu se středem a, pak se v y musí vyskytovat přesně člen (x − a); už jsme také viděli, že násobící konstanta navadí. Toto pozorovnání nás přivádí k následujícímu algoritmu.

Jak rozvíjet.
Krok 1. Identifikujte, která řada bude základem pro vaši expanzi, vzhledem k tomu, že se může použít substituce a násobení vhodnou mocninou. Utvořte plán.
Jsou tři typické situace.
•• Daná funkce je v zásadě jednou z funkcí, jejíž rozvoj už znáte, s malými modifikacemi. Pak je to už jen otázka přepisu dané funkce do vhodného tvaru, jak je vysvětleno v Kroku 2.
•• Daná funkce se skládá z funkcí, které už známe (s mírnými modifikacemi), spojených operacemi. Pokud nelze použít nějaký trik, tak to znamená, že se musí rozvést každá z těch funkcí a výsledné řady se pak musí poskládat dohromady. To může být problém, pro typické situace viz tato poznámka.
•• Daná funkce má části, které nelze řešit pomocí předchozích přístupů. Pak je třeba se podívat po nějaké fintě. Často se dají použít vlastnosti mocninných řad, jmenovitě fakta o derivování a integrování řad. Když zderivujete či zintegrujete danou funkci (nebo její problémovou část), dostanete něco, co už umíte (s modifikacemi) rozvinout? Pokud ano, pak použijte tento rozvoj a poté zopakujte pozpátku postup, který vás tam dostal (viz Příklad níže). Toto se nejčastěji používá při rozvojích logaritmu či u výrazů jako 1/(A + x)², obojí vede na geometrický rozvoj.

Krok 2. Po Kroku 1 už je známo, která funkce bude použita jako základ pro rozvoj, ale před vlastním rozvojem je nutno ji přepsat tak, aby se v ní všechna x objevila jako výraz (x − a).
Během tohoto procesu se obvykle objeví nějaké nechtěné části; zbavte se jich pomocí algebry a identit, abyste se ve chvíli, kdy se opravdu rozvíjí, dokázali dostat ke známým funkcím substitucí. Pak použijte ten rozvoj (ty rozvoje).
Typické situace ukážeme na těchto příkladech, které také poslouží pro následující kroky.

Studenty obvykle nejvíce trápí rozvoj pomocí geometrické řady. Onen příklad už ukázal, jak postupovat. Nejprve se vytvoří člen se správným středem. Pak přepište výraz tak, aby byla konstanta ve jmenovateli vpředu a za ní bylo mínus. Nakonec tuto konstantu vytkněte. Všimněte si také, jak jsme v prvním příkladu vytvořili správný střed u polynomu 2x.

Krok 3. Upravte výsledek tak, aby nakonec byla jen jedna mocninná řada.
To obvykle znamená vyndat konstanty A ze substituce ven ze členů (Ax − B). Další často používané operace: násobící členy před řadou se přesunou dovnitř, řady jsou sečteny. Někdy také musíme řady násobit, dělit, derivovat či integrovat. Připomeňme, že při sčítání řad je třeba nejprve upravit mocniny a indexaci, aby se shodovaly (viz Úpravy (mocninných) řad v části Přehled metod - Řady funkcí).

Krok 4. Určete oblast, na které platí výsledný rozvoj.
Toto je rozhodnuto v kroku, při kterém se ve výpočtu objevila řada. Tento krok byl platný pouze pro jisté hodnoty y, z čehož se snadno najdou omezení pro x.

Ukážeme teď jeden příklad, bude trochu delší, aby ukázal více různých postupů (některé méně příjemné). Pro další příklady viz Řešené příklady - Řady funkcí.

Příklad: Rozviňte v řadu se středem a = 1 funkci

Jaký je plán? Evidentně budeme muset rozvinout logaritmus v řadu se členy (x + 1). Někteří lidé si to pamatují, ale jiní ne, tak zde tento rozvoj nějak zkusíme odvodit. Není způsob, kterým bychom dokázali dostat logaritmus z těch čtyř základních funkcí pomocí algebraických operací, takže toto nepomůže. Logaritmus je inverzní funkce k exponenciále, jejíž rozvoj známe, ale Lagrangeův inverzní vzorec je tak odpudivý, že si to necháme jako poslední (zoufalou) naději. Klíčové je pozorování, že když zderivujeme logaritmus, dostaneme 1/x, což je něco, s čím už se dá pracovat pomocí geometrického rozvoje. Z tohoto rozvoje se pak dostaneme zpět k logaritmu integrací a jsme hotovi.

Když tak rozvineme logaritmus, zbývá jen nějak zapojit dělení členem x. Jsou v zásadě dvě možnosti. Jedna je vzít daný výraz jako součin logaritmu a 1/x. Obojí umíme rozvinout a pak se použije Cauchyho součin. Druhá možnost je rozvinout samotné x a pak použít algoritmus pro dělení řad. Ukážeme oba způsoby. Máme tedy zformulovanou strategii a můžeme se do toho dát.

Nejprve rozvineme logaritmus. Začneme rozvojem jeho derivace.

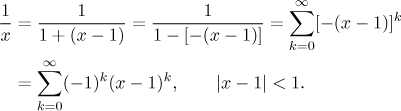
Jsou dva způsoby, jak dostat logaritmus z 1/x. Můžeme tento rozvoj přepsat pomocí proměnné t a pak na obě strany aplikovat určitý integrál od řekněme 1 do x. Druhá možnost je integrovat obě strany pomocí primitivních funkcí, pak je tu ale problém konstanty. Pořád je to ale asi snažší než tím určitým integrálem.

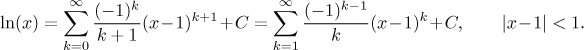
Posunuli jsme index nahoru o 1 ("nové" k je dáno vzorcem k + 1), abychom upravili exponent v mocnině. Jak najdeme to správné C? To je snadné, tato rovnost by měla platit pro všechna x z vyznačené množiny, takže můžeme dosadit například x = 1 do obou stran a zjistíme, že C = 0.

Teď je načase do toho zapracovat dělení členem x. Nejprve přístup přes součin řad. Máme náhodou štěstí a ušetříme čas, protože už víme, jak rozvinout 1/x.

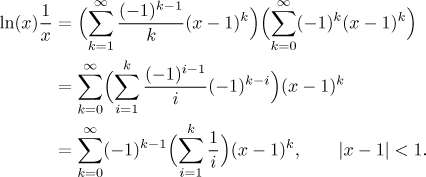
Toto je typický výsledek z Cauchyho součinu. Známe nějaký vzorec pro částečné součty harmonické řady, abychom tak mohli zapsat koeficienty řady nějak lépe? Ne, takže to necháme, jak to je. Teď ten druhý přístup.

Polynom x má jako svůj rozvoj se středem 1 řadu 1 + (x − 1). Navíc víme, že je tato funkce "pěkná" v 1 (nedělíme nulou), takže podíl bude mít také nějaký rozvoj v 1, napíšeme tam obecnou řadu. Dostaneme

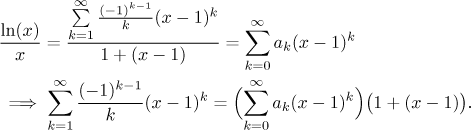
Obvykle bychom potřebovali napravo použít Cauchyho součin, ale zde nám vlastně stačí jen výraz zjednodušit a zapsat jako jednu mocninnou řadu.

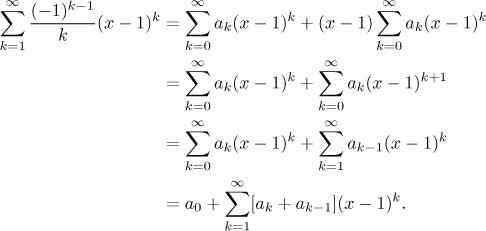
Teď máme dvě řady, které se rovnají, takže podle jednoznačnosti rozkladu se musí jejich koeficienty rovnat. Dostáváme systém rovnic

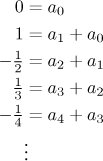
Máme tedy a₀ = 0, a₁ = 1, a₂ = −1 − 1/2, a₃ = 1 + 1/2 + 1/3, a₄ = −1 − 1/2 − 1/3 − 1/4. Tímto způsobem můžeme dostat, kolik koeficientů chceme. Jsou to stejné koeficienty jako předtím a máme stejný problém, nejsme je schopni vyjádřit pěkným vzorcem. Někdy máme štěstí a dostaneme vzor, který umíme rozeznat, pak si tipneme vzorec pro obecné k a dokážeme jej indukcí. Dnes ale ne.

Sčítání mocninných řad
Zpět na Přehled metod - Řady funkcí