Applications of series

Of course, there are many applications, but lots of them are too advanced and we could not even start explaining them with the level of knowledge we have here. For instance, series can be quite helpful when solving differential equations, in fact Fourier series were developed to do exactly this, but for that you will have to wait for some course on differential equations. Here we will look at several applications that are easier or at least that can be explained reasonably well. We start with a general idea of using the Fourier series for frequency analysis (we actually get to mention mp3 there). Then we pass to power series. We start with some examples how power series can help with calculations, from this we naturally get to the Gaussian integral. One may argue that both these topics are more history than present, so we look at evaluation of functions, which is something that you use every time you punch a button on a calculator or want some evaluation from a computer. We conclude with a quick look at finding pi.

Fourier series and frequencies

The basic idea of Fourier series is that we try to express the given function as a combination of oscillations, starting with one whose frequency is given by the given function (either its periodicity or the length of the bounded interval on which it is given) and then taking multiples of this frequency, that is, using fractional periods. When we look at coefficients of the resulting "infinite linear combination", we can expect that if some of them are markedly larger then the rest, then this frequency plays an important role in the phenomenon described by the given function. This detection of hidden periodicity can be very useful in analysis, since not every periodicity can be readily seen by looking at a function. In particular, this is true if there are several periods that interact.

Imagine that a function f describes temperatures at time t over many many years. There is one period that should be easily visible, namely seasonal changes with period one year. We also expect another period going over this basic yearly period, namely 1-day period of cold nights and warm days. Now the interesting question is whether there are also other periods. This is very useful to know, since such knowledge would tell us something important about what is happening with weather and climate. Frequency analysis offers a useful tool for such an investigation, looking over long data sequences it may point out cold ages and other long term changes in climate.

There are areas where decomposition into waves comes naturally, for instance storage of sound. When we are given a sound sample, Fourier transform allows us to decompose it into basic waves and store it in this way. Apart from data compression we also get further memory savings by simply ignoring coefficients that correspond to frequencies that a typical human ear does not hear. This is the basis of the mp3 format (it uses transform that is something like a fourth generation offspring of cosine Fourier series).

Fourier decomposition can be also generalized to more dimensions and then it can be quite powerful in storing visual information - it is for instance the heart of the system used by F.B.I. to store their fingerprint database. Since this decomposition is so useful, one important aspect is the speed at which we can find the coefficients. This inspired further development and today we do not usually use the standard Fourier series but its more powerful offspring, for instance something called Fast Fourier Transform (FFT). Here also hardware helps, there are devices (integrators) that have this wired in, roughly speaking one feeds it a function and the device spits out a Fourier coefficient.

In conclusion, Fourier decomposition is something you meet every time you listen to mp3 music (or the police take your fingerprints).

Power series used to be not just important, but crucial in days before calculators came around. Functions were replaced by their Taylor series in calculations, or by their finite parts - polynomials. Engineers used to remember expansions for many functions and used them freely. For instance, instead of calculating limit using l'Hôpital's rule

one can do this trick, which an experienced engineer would do in his head (see this problem in Solved Problems - Series of functions).

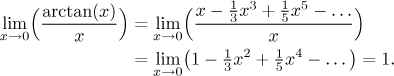
Of course, without uniform convergence this can be tricky, but here we do have it. I have met a limit which had unpleasant products in it, so using l'Hôpital's rule made it grow, after four l'Hôpitals the expression in the limit exceeded the length of the line and I gave up. Then I replaced all sin(x) by series and it was done almost immediately.

Another example: If we want to know what is the multiplicity of x = 0 as a root of f (x) = 1 − cos(x), we can go by definition, or we can do this:

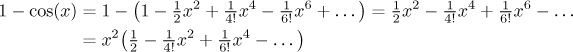
and multiplicity is clear.

These were trivial examples, but similar tricks help a lot also in more involved calculations. There is a rather interesting story dating back to the World war 2. Developing the atomic bomb required very complicated calculations and they simplified them using series to lots of additions and multiplications. The problem was then solved by stuffing a room full of (mechanical!) addition and multiplication machines and devising ingenious ways of moving calculations through them. I heartily recommend one of Feynman's reminiscences for further reading.

At least 90 percent of all statistical calculations are based on knowing the so-called "normal distribution", which basically means that we need to know how much is the integral

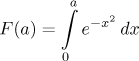
for positive a. Unfortunately, it is a known fact that the antiderivative of the function f (x) = e^−x2 exists but it cannot be expressed using elementary functions and the usual operations (including composition). There are two possible approaches to this problem. One possibility is to use numerical approximation of the above definite integral, but that would have to be done for every a from a reasonably dense set, which is quite a lot of work. The other possibility is to find an expression for F(a) and then evaluate it directly. Series offer a nice way to do it. We start by expanding the exponential.

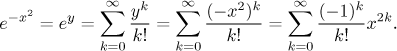
Now we integrate.

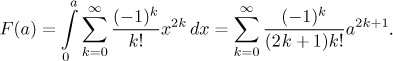
This series converges for every a, so we just evaluate as many terms as we need to get the desired precision. Since people working in statistics need this a lot, these values are gathered in thick books of distribution tables, algorithms for evaluating it were also implemented in statistical software.

A similar calculation helps us to solve this problem in Integrals - Solved Problems - Integrals.

Human mind and processors can do basic algebraic operations - addition, multiplication, subtraction and (with a bit of effort) division. If we need a value that cannot be obtained by combining these basic operations, we are in trouble and so are calculators/computers. How do we calculate the fifth root of 2? How do we get ln(3)? How about e^2.9?

The natural answer is series. For instance, we have a nice series for the exponential. However, this brings another problem. Calculator needs to know how many terms of the series it should evaluate, but the series converges slower as x grows. Fortunately a simple algebraic trick can help. We write x as x = n + r for an integer n and some number r from the interval [0,1). We know that

e^x = eⁿ⋅e^r = e⋅e⋅e⋅...⋅e⋅e^r.

Since multiplication is not a problem and the number e itself is stored somewhere, we see that it is enough to know how to find e^r for r < 1. The series for the exponential converges uniformly on [0,1), so we have its concrete truncation which gives good approximation for all such r.

Logarithm is a similar case, we have a series, but now the main problem is not speed. The series for logarithm does not even converge for large x, we can use it only for x < 2. Here we use the following algebraic simplification. We write x as x = 2ⁿ⋅r for an integer n and some number r from the interval [1,2). We know that

ln(x) = nln(2) + ln(r).

Again we see that in fact we only need to know logarithm of a small number for which we have a series.

Here another trick is often used to speed up calculations. There are more series for logarithm and these two look quite similar.

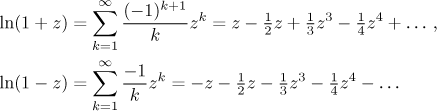
When we subtract them, we get an interesting formula

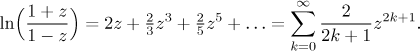
This series converges much faster, since it skips every second term. The calculations then go as follows. First we decompose x into n and r as above. Then we find z such that

Then we evaluate this fast series above. The restriction on r (we take only numbers between 1 and 2) means that z is taken from the interval [0,1/3) and the series converges uniformly there, so again we know how long the partial sum should be to approximate well enough throughout all these z.

Once we have logarithm and exponential, we can use them to find other things, for instance the general power A^B.

Pi is a transcendental number, which means that we cannot express it using algebraic operations. One way to evaluate it is offered by series. If we use the series for arctangent that we already saw above, we get

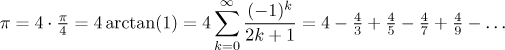
We can add up as many terms of this series as we need to get the desired precision. Actually, this series is quite bad, since it converges very slowly; various tricks are used to make it converge faster.

Similarly, the expansion of exponential offers a way to find the value of e.

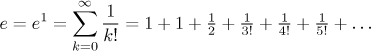
Since this is in a sense the last section of Math Tutor, I think that I can afford to end it with a story. When I was at high school, we had problems with lockers security and student guards were instituted by the management. One day it was my turn, I was supposed to sit in the locker area for several hours with my friend and basically do nothing. We shared the disability of liking mathematics and we decided to find the number e with 50 digits precision. We took two large sheets of papers and one worked as a "dividing machine", the other as an "adding machine".

The "dividing machine" started with 1 on the first line. Then he divided this by 2, obtaining the line 0.5000. On the next line he divided this by 3, obtaining 0.16666666666666... (fifty digits). He continued in this way, on every line there was the number 1/k! needed for the series.

The "adding machine" started with 1, then added the first line from the divider's sheet, then added the second line from the divider's sheet etc. When the divider arrived at a line of fifty 0's, we were done. In this way we survived the boring hours. Eventually we found an "official" value of e in some book and it turned out that we made a mistake somewhere around the 30th decimal place. Before mechanical devices came around, this is the way calculations were made, hundreds of people called "calculators" sat in badly lit rooms spending their time doing boring calculations. For us it was an interesting experience.

Back to Theory - Series of functions