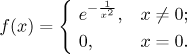
Here we explore Taylor things for the function

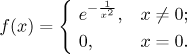
Let us say right from the start that this function is not weird or ugly, it is a nice function. After all, the expression in the definition is just a composition of an exponential (the best function around) and a power, there is nothing fishy about e^−x−2. Since it has limit 0 at 0, it is possible to define f at 0 in such a way that it becomes continuous. It looks like this.

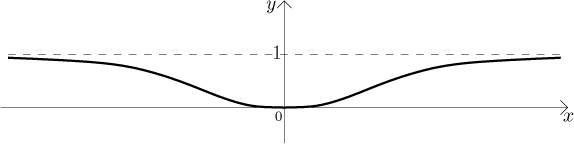
When we ask about the usual properties, we find that this function pretty much has them all, it is about the nicest function possible, since it has continuous derivatives of all orders everywhere. Because this will be important below, we will prove this assumption and actually give a better specification of this result.

Claim.
For every positive integer k there is a polynomial P_k(x) of degree at most 2k − 2 such that for non-zero x we have

Such a statement is usually proved using mathematical induction.

k = 1: We find the first derivative in the usual way and just out of curiosity, we also show the second derivative.

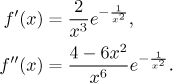
In both cases it works, the form is as prescribed in the Claim.

Now we should prove the induction step. We assume that this Claim is true for k and we will show that then it must be also true for k + 1.

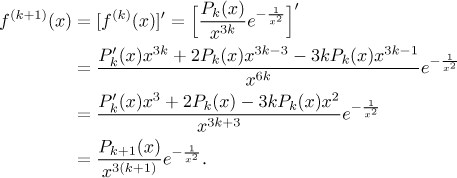
By our assumption, deg(P_k) ≤ 2k − 2, then deg(P_k′) ≤ 2k − 3 and consequently deg(P_k+1) ≤ 2k = 2(k + 1) − 2, which concludes the proof.

The estimate on the degree of the numerator is important for the following reason. We actually just need to know that its degree is less than the degree in the denominator, so when we divide the polynomial, there will only be terms of the form 1/xⁿ. Thus there is a polynomial Q_k such that the k-th derivative is equal to Q_k(1/x)e^−1/x2. Using this we get the following result.

Claim.
For every positive integer k we have

Indeed, it is enough to apply substitution

Then repeated l'Hôpital's rule yields zero, see scale of powers, similarly we work out the limit at 0 from the left. This substitution can also simplify differentiating f, see Remark at the end.

This claim shows that the function f also has derivatives of all orders at the origin and they are zero. This means that the graph of this function is extremely flat at the origin. Recall that if we want to find the Taylor polynomial/series with center 0, we use exactly these derivatives to find the coefficients. Thus we get the following conclusion.

Fact.
The function f has Taylor polynomials of all orders with center a = 0 and the Taylor series with center a = 0 and

What does this mean? First, since the given function is not zero except at the origin, it follows that (apart from the center 0) the Taylor polynomials do not approximate the original function f well, in fact they do not approximate it at all. This is despite the fact that f is smooth, with derivatives of all orders everywhere, so from the usual point of view it is "nice".

Concerning the series, the Taylor polynomials converge - as partial sums of the series - uniformly on the whole real line to T. Thus the series is again the best possible, but it is definitely not equal to the original function f. Recall that we had a theorem that guaranteed good convergence of series if f has uniformly bounded derivatives on some neighborhood. This is obviously not true here, there is no neighborhood of 0 on which all derivatives would be uniformly bounded.

This shows that the problem of approximation of functions by power series can be quite tricky even for nice functions.

Remark: The substitution y = 1/x can also help in working with the derivative. First, observe that

y′ = −1/x² = −y².

Now we just apply the chain rule to find that

f ′(x) = [e^−y2]′ = (−2ye^−y2)⋅y′ = 2y³e^−y2.

Similarly

f ′′(x) = [2y³e^−y2]′ = (6y² − 4y⁴e^−y2)⋅y′ = (4y⁶−6y⁴)e^−y2.

When we substitute y = 1/x into it, we get exactly the derivatives that we obtained above, but we could do without the quotient rule. In this way it is also easier to prove by induction that the k-th derivative is equal to Q_k(y)e^−y2 for some polynomial of degree at most 3k. We also get right away the form that helps with calculating limits.