Box "substitution"

Substitution rarely solves problems by itself, but it is used to simplify them and to move problems from one place to another. It is actually a general method. For sequences, the basic idea is as follows: We have a sequence {a_n} in which n is always inside a certain expression, call it f (n). We want to find a limit of this sequence. If the expression f (n) satisfies certain assumptions (which are reasonable and natural), we can replace this expression with a new letter (say, m) and obtain an easier problem.

We start with a very simple example: Find

Since the expression 2n² appears every time we have n, we can give this expression a new name, say m. We get a new limit:

Although it did not help very much, the problem is essentially the same (so the methods to solve it would also be essentially the same), this new limit looks much easier and calculations will be most likely simpler.

Note that the replacement of 2n² with m was not just as simple as it looks, there is more behind it than meets the eye. In particular, note that the new limit has m→∞ written under the "lim". This makes sense, the new expression has no n in it, so the notation should fit. But we cannot just change letters, this change has to follow from the substitution equality m = 2n². To be precise, we have to check that if n→∞, then indeed m = 2n²→∞.

Now we are ready to state formally the requirements needed for a substitution m = f (n) to work. First, the numbers f (n) must be integers for n integer. Second, the sequence {f (n)} must go to infinity as n goes to infinity. If this is satisfied, we can change the limit from n to m. We replace all appearances of f (n) by m, we also have to change n to m in the limit symbol.

However, substitution can be used also in more general situations, the chosen substitution equality m = f (n) can be used to replace also other formulas featuring n then just f (n). Substitution in general (for limits of sequences) works like this:

Substitution:
Step 1. Decide which expression f (n) should be substituted for, set up the basic substitution equality m = f (n).
Step 2. Check that if n is a natural number, then also m = f (n) is an integer, and that m→∞ if n→∞.
Step 3. Use the equality m = f (n) to find the appropriate formula for n, and/or other expressions appearing in the given sequence. All these calculations are traditionally done between vertical bars (see the example below).
Step 4. Transform the given limit into the new language of m. All appearances of n must be replaced, in the given sequence we replace it using the equality m = f (n) and formulas deduced from it, in the "lim" picture we simply write m for n.

And that's all.

We noted that the new limit problem is basically of the same kind as the original one, substitution just makes it easier to write (which in itself is often worth doing it). However, there are problems where substitution can help even more, like in the following example.

Example: In this following example we use substitution to move addition from denominator (where we cannot do anything about it) to the numerator, where it can be handled by algebra. Note the way we write the substitution. Putting the formulas between vertical bars is not standard, but it is used quite widely. We will also put comments between double angled braces as usual.

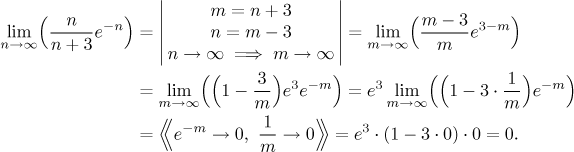
Note that we pulled e³ out of the limit, since it is a multiplicative constant and as a such it can be factored out, making the limit easier.

Note: This method is also used when finding limits of functions. In fact, when evaluating limits of sequences, one often draws on methods from the theory of functions (see Sequences and functions in Theory - Limits). Then it is not exactly necessary to require that the expression f (n) gives an integer and goes to infinity. But then, after performing the substitution, one obtains a limit problem for functions, not sequences. However, the answer will also work for the given sequence. We will show it on a simple example:

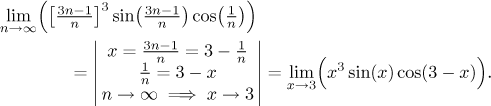
We should actually be able to find the limit directly, but we wanted to show how the substitution works. Note that if we needed it, we could calculate n = 1/(3 − x) and use it. Note also that in fact we have x→3^- (x tends to 3 from the left; sometimes we need to know this).

Next box: 1/0
Back to Methods Survey - Limits