Problem: Evaluate the following limit (if it exists)

Solution: When we try to substitute infinity, we get infinity in the denominator, which is a good start, but in the numerator we get an indeterminate expression ∞ − ∞ under the root, then another infinity subtracted, so we cannot really say what type we get there.

When we look at the given fraction (ignoring the cube on the outside, it is a "nice" outer function that can be pulled out of the limit), we notice that it features powers and roots; that is, it exactly fits the box "polynomials and ratios with powers". Could we determine the answer intuitively?

We should start inside the root and observe that the fourth power prevails over the cube inside. Thus the term "−2n³" can be ignored when n is huge. What do we get then?

Unfortunately, we got two matching dominant terms in the numerator that are subtracted, which means that the intuitive way would not give an answer, we are not allowed to cancel them in a case like that. What if we try to keep them and solve the problem by factoring out dominant terms, which is the recommended way to handle mixed powers? Unfortunately, in the case of matching dominating terms that are subtracted we obtain ∞⋅0. Indeed, factoring out the dominant term (starting with the root) we get

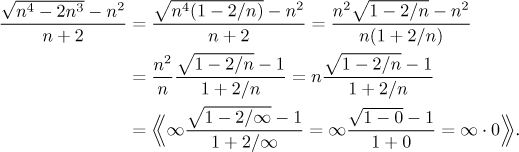
Thus we need to cancel the dominant powers precisely (algebraically), not in a simplified way, and the form of the sequence hints at the right box, "difference of roots"

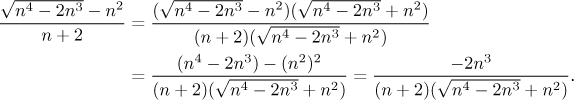
We obtained a different expression of the "ratio with powers" type, in which we were able to substract the two dominant terms in the numerator. Unless we are really unlucky, we should be now able to apply the intuitive calculations and get the answer.

So it worked, we guess that the answer is (−1)³ = −1 (we should not forget the cube!). How do we write it properly? First we pull out the cube, then do the algebra part (we can just copy the answers we already got above). Then we factor out the dominant powers (thanks to our intutitive calculation we know that the dominant power is n³ on the top and bottom, and in the denominator it comes from two sources) and finally get the answer:

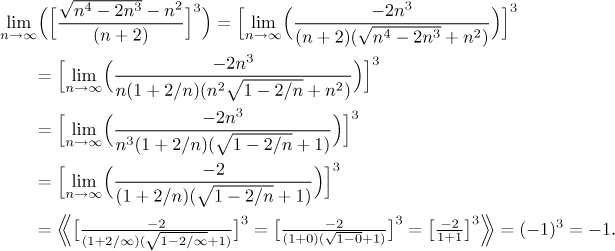
Is there an alternative? After pulling out the cube we are left with a fraction of the type "something over infinity" (we now pretend that we do not know how the numerator worked out above), which means that the more general form of l'Hospital's rule could be used (see the box "indeterminate ratio"). Note how fortunate it is that we do have this general form. If we wanted to use the usual l'Hospital (infinity over infinity), we would have to investigate the numerator and try to show that it tends to infinity. So let's look at the fraction; we know that to use l'Hospital we have to pass to a function problem:

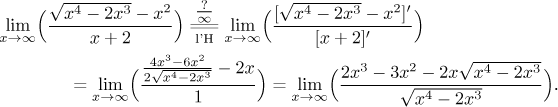
We obtained an expression that is not really nicer than the one we started with. This shows one typical feature of the l'Hospital rule: it is not good in getting rid of square roots. Indeed, if we tried another l'Hospital, the root would still be there, and again, and again. It is possible that after some, say, five l'Hospitals we would get an answer, but obviously this is the time to try something else. Good that we did not waste time on analyzing the numerator.

Next problem
Back to Solved Problems - Limits