The basic type of a sequence we will cover here is polynomials - that is, linear combinations of powers na - and linear combinations of related expressions (exponentials, general powers, factorials, logarithms). Some parts of such linear combinations can be also under roots. Typical example:
![]()
How to find limits of such expressions:
Step 1. Identify the dominant term of the given expresion, start by handling individually all roots: Determine the dominant term of the expression under the root, then apply the root to it; this will determine the type of the root as a whole. Then compare types of roots with other types in the sum and identify the dominant term. For determining dominance, use the scale of powers:
Every type prevails over the types listed later:
(1) the power nn,
(2) the factorial n!,
(3) the exponential qn,
(4) the power na,
(5) the logarithm
Within each category, terms with larger q, respectively a
prevail over those with smaller parameter.
For practical use people often prefer a more colloquial way of remembering this hierarchy, using phrases like "powers beat logarithms" and "exponentials beat powers" etc. For details, see Intuitive evaluation in Theory - Limits, especially this remark. When determining dominance, we ignore constants by which some powers, exponentials etc. might be multiplied.
If we want to just quickly guess the outcome, the dominant term tells us how the whole expression will behave at infinity - but now it is necessary to consider ultiplicative constants in this guessing. If there are more terms of the dominant type in the given expression, see below for the rule on putting them together.
Step 2. If there is a unique dominant term, factor it out and then find the limit of the resulting expression. If there are more dominant terms, they can be put together only if it does not result in disappearance of this dominant term. The procedure of factoring out still works.
If there are more dominant terms and putting them together would make the dominant type disappear entirely, then the sequence has to be handled differently. Usually one tries to cancel the dominant term using algebra. The most frequent reason why terms could not be cancelled is that some are mixed up in roots. In such cases, try the box "difference of roots".
Sometimes one has to simplify using algebra to identify the types of terms properly.
Example:
Consider the sequence above. First we address the root. Under the root
there are two powers of the type na (the second one
is trivial,
Now we look at the whole sequence. There are three terms, a square, a root (which is in fact of the type n), and a logarithm (we are ignoring the multiplicative constants now). Powers beat logarithms, so the logarithm can be ignored when n is large, and of the powers, the higher one wins. We just concluded that n2 is the dominant term. Thus we can deduce how the whole expression behaves (now we doconsider the multiplicative constants).
![]()
We just concluded that when n grows large, the given expression
behaves just like
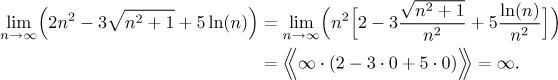
How did we find that the two fractions on the right converge to 0? The first by algebraic simplification, the second using l'Hospital's rule, see here. Note that it is often easier to start factoring under roots and work your way out rather than factor out of the whole expression at once.
Often we encounter fractions where the numerator and denominator are of the above type. Then the procedure is as follows:
Step 1. Find the dominant terms of the numerator and denominator as above.
Step 2. Factor out the dominant terms, then cancel if possible and find the limit of their ratio.
Sometimes it is easier to use an alternative:
Step 2'. When the dominants of the numerator and denominator are the same, cancel both the numerator and the denominator by the dominant. People actually use cancelling also in other situations, the rule "cancel the smaller dominant" is often quoted, but has a "little" drawback: It often does not work. If you want to find out more about cancelling in ratios, check out this little note.
Example: Evaluate (if it exists)
![]()
The second term in the denominator is not of the proper form, so first we simplify it:
![]()
Now we are ready to look at it: In the numerator, the exponential 4n is the dominant term, the same term is dominant in the denominator. If we used factoring, we would get
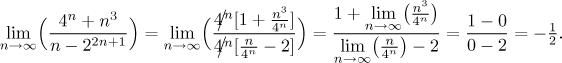
The limits of the fractions at the end are easy to find using the l'Hospital rule.
Cancelling is a bit faster:
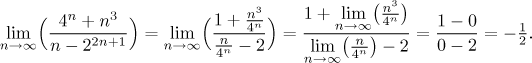
As it is written it looks about the same, the difference is in the mindset when writing it. It is a matter of personal preference and psychology, some people prefer to think of pulling a common factor out, which often means dividing some term by it, other people find it easier to think in terms of "divide everything you can see by this term".
When expressions of the above type are multiplied, one can determine the dominant term (the type) of each part, putting them together would determine the type of the whole product. However, without luck it is likely that the resulting type will not be a part of the scale of powers, but a combination of more such power types. The final outcome then cannot be determined by rules covered here, a lot depends on experience and intuition.
In Solved Problems - Limits, these methods are used in this problem, this problem, and this problem. A more involved example is this one.
Next box: difference of roots
Back to Methods Survey
- Limits