Problem: Evaluate the following limit (if it exists)

Solution: First we try to plug in to determine the type (and if we are lucky, the answer). We get

In order to find out what the whole sequence behaves like, we should first tackle the indeterminate fraction, but this one is actually simple. Since it is a ratio of polynomials, we can use the tricks from intuitive evaluation in Theory - Limits to guess the answer:

This answer can be confirmed by factoring out, but there is no need to hurry. Why? After we confirm that the fraction goes to infinity, we would get info only about the second part of the given sequence. The first part goes to zero, so together we get 0⋅∞. This is an indeterminate form, so we have to work on it and the calculations that we would have done for the second part would be useless anyway. There is an appropriate box for indeterminate product, it says there that we should change the product into a ratio and check on it. Which part do we "put under"? The exponential seems the better candidate, since there we just change the sign in the exponent (look here to see what would happen if we try it the other way):

We were able to determine the type so quickly since we worked out the ratio of polynomials above. Now we have an indeterminate ratio that looks standard, so without further ado we switch to functions and apply the l'Hospital rule.

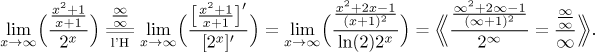
Now we have another problem. What is the type of the top fraction (the numerator of the main fraction)? In fact, we need not necessarily care, because the l'Hospital rule can be applied to the type "anything over infinity", which we have here, but taking derivative of the top fraction does not look too appealing. So we look at it closer, hoping that we get some answer that would allow us to avoid another l'Hospital. It is a ratio of polynomials, so we try the tricks from the appropriate box. First we determine the dominant powers, multiplying out the denominator should help. Then we should factor out dominant terms, but they both turn out to be n². When the leading powers in a fraction are equal, it is usually easier to just cancel this power:

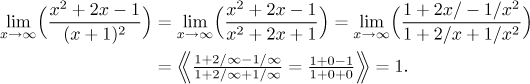
So now we know that the fraction on top goes to 1, and we can finish the problem:

Is there any way to simplify this calculation? Well, one cannot avoid the l'Hospital rule, but it can be made a bit easier. How? We know that the derivative of a fraction is quite beastly, but the product rule gives nicer results. So we try to rearrange our sequence a bit before we get to l'Hospitaling:

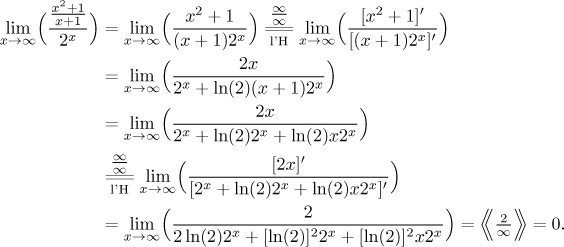
This time we had to use the l'Hospital rule twice, on the other hand it was perhaps a bit easier from algebraic point of view. It's up to you which way you prefer.

We can also try something completely different. When we wrote it as one fraction, there were only powers and exponentials, so we could try to apply tricks from the box polynomials and ratios with powers. There might be trouble with the product in the denominator, but it will actually work out when we try to intuitively guess the outcome:

We used the fact that "+1" can be ignored when compared to powers and that "exponentials beat powers".

How do we confirm this guess? The usual way, by factoring out the two dominant powers and the exponential, then we apply the l'Hospital rule.

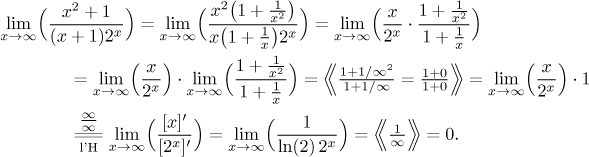
This was perhaps the easiest solution.

Next problem
Back to Solved Problems - Limits