Problem: Evaluate the following limit (if it exists)

Solution: First we try to put in infinity. Note that for n we put positive numbers, so 1/n > 0; therefore 1/n tends to 0⁺ in the limit algebra.

Recall that 1/0 is an expression whose outcome cannot be decided and must be investigated closer, which is why we needed to figure out that the zero is actually 0⁺. The fact that sin(0⁺) = 0⁺ we either remember or we argue like this: First, we know that sin(1/n)→0. Second, when n is a huge natural number, then 1/n is a very small positive number, so sin(1/n) > 0. These two facts mean that sin(1/n)→0⁺ as claimed.

Anyway, we did not find the limit, but the attempt told us that this problem belongs to the box indeterminate difference. The standard solution calls for some way to change this into a fraction. We will try to create a common denominator.

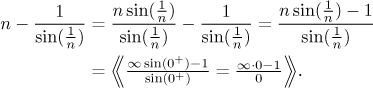
We would like to appeal to Mr. l'Hospital, but unfortunately, it does not apply to type "something over infinity". We need to find out what is in the numerator; that is, first we need to find out the limit of the product n⋅sin(1/n). What are the possibilities? If it gives 1, then the whole ratio will be of the type "0 over 0" and we know what to do. If it gives other number than 1, say, a (including plus or minus infinity), then the whole ratio will be of the form (a − 1)/0⁺, which is +∞ (if a > 1) or −∞ (if a < 1), so we would get the answer right away. Finally, if the product n⋅sin(1/n) does not have a limit, we have a non-typical problem and would have to investigate the whole fraction in some specific way.

How do we find out what is the limit of n⋅sin(1/n)? We saw that it gives ∞⋅0, so the appropriate method will be found in the box "indeterminate product". The procedure calls for changing the product into a fraction and then applying the l'Hospital rule, since we will for sure get an indeterminate ratio. Which part of the product should we "put under"? Since the sine is already complicated enough, it would not be very wise to make it still more complicated by adding the power ⁻¹ to it (see here what happens if you try it). So we put down the power and pass to functions right away, we will need it for the l'Hospital rule anyway.

Note how we sometimes write 1/x (when we are substituting infinity, this form is more intuitive) and sometimes x⁻¹ (when taking derivative, this form is better). Anyway, now we know that the product gives 1 and we can return to the original fraction. We now know that it is of the form "0 over 0", so we apply the method recommended in the box indeterminate ratio: we pass to functions and apply the l'Hospital rule:

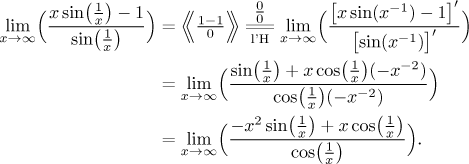
What is this expression? Substituting infinity yields

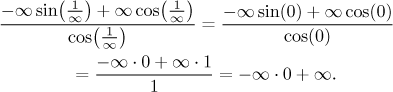
We have a problem again. We should first investigate the product of x² and sine, and just like above (changing it into a fraction, applying l'Hospital) we find that it goes to infinity. Smarter approach would just use the above calculations like this:

x²sin(1/x) = x⋅xsin(1/x)→∞⋅1 = ∞.

In any case, what we got overall is the fracion "infinity minus infinity, that all divided by 1". The division by 1 is no problem, so it is probably best to simply take it out of the expression and evaluate it separately.

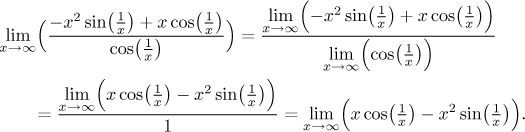
We are left with the "infinity minus infinity" part. We are supposed to make it into a fraction and apply l'Hospital, hoping that this time we get something decent. However, now there is no obvious common denominator. What do we do?

One possibility is to use the universal trick for changing difference into a fraction. It leads to terrible things, as you can see here.

A smart student would notice that if one x was taken away from the expression, there would appear xsin(1/x), someting that we already know goes to 1. Does it help?

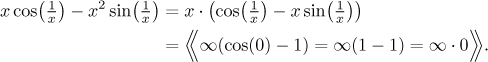
We see that we obtained an indeterminate product, and there is even an obvious candidate for "putting under". Here we go:

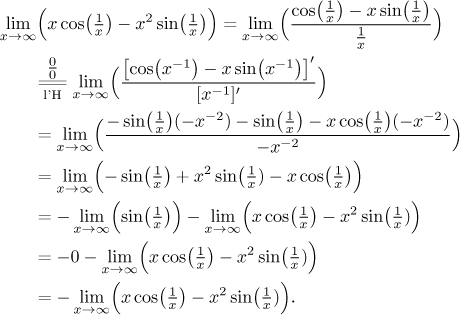
Surprisingly we got the same limit, just with the opposite sign. What does it mean?

First of all, this shows that the method we tried does not help, repeating the l'Hospital trick would just change the sign again. Was there any moment in our calculations where we had another option? None that we would see. This "direct" way therefore cannot tell us more.

The fact that after applying the l'Hospital rule we obtained the same limit, just with the opposite sign, is strange. Can we use it to get at least some information? Yes. If there is no limit, we obviously cannot say more. What happens if this limit does exist and is equal to, say, L? The above equation then reads L = −L, that is, L = 0. Note that L cannot be infinity or negative infinity, since these two do not satisfy L = −L. So here is the conclusion so far:

Either the given limit does not exist, or it must be equal to zero.

If we want to solve this problem, we need to take a different track right from the start. How about this: Indeterminate differences can be often solved by changing them into products, usually indeterminate. Here we would do it this way:

The standard procedure for an indeterminate product is to change it into a ratio, which usually leads to l'Hospital's rule. Let's try it.

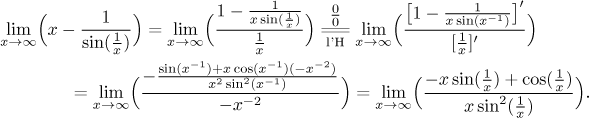
This looks quite bad, essentially this is another blind alley. What can we do? The key to success is the observation that in both methods the trouble is caused by the x that keeps interfering with 1/x. However, in both cases we can change the investigated expression so that it only features 1/x. L'Hospital's rule then leads to substantial simplification. The first approach goes like this:

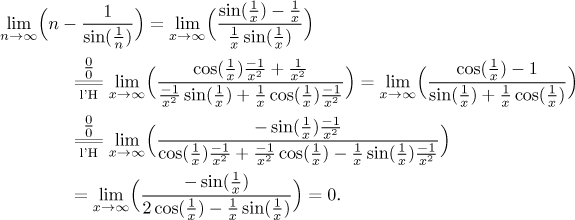
The second approach goes like this:

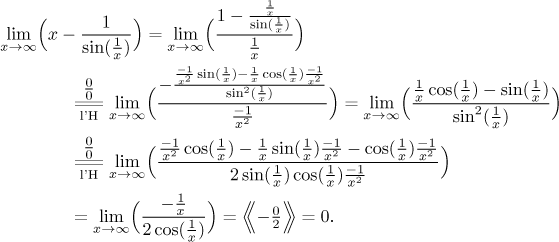
Both is quite dreadful, but it does give us the answer. Nevertheless, once we get 1/x everywhere, an experienced limiteer would immediately think of substitution.

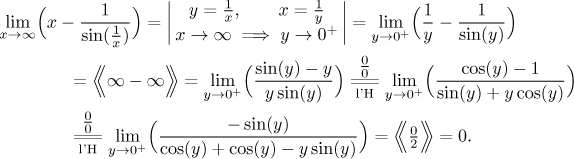
This is most likely the best solution.

Next problem
Back to Solved Problems - Limits