Problem: Evaluate the following limit (if it exists)

Solution: What happens if we put infinity into this expression? We know that sin(n) does not have a limit, so using the limit algebra we get

If we had only the usual l'Hospital rule and hoped to use it, we would have to prove that the numerator tends to infinity. This is actually true (see below), but fortunately we have the general version, too, that applies to "something over infinity", so we do not have to do more analysis and apply it right away (after changing to functions):

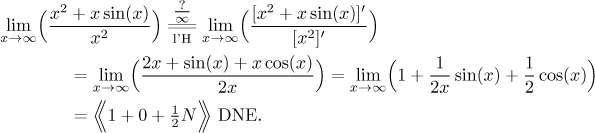
How did we get that "0" in the last line? We have a rule "zero times bounded gives zero" (see the box comparison and oscillation), which exactly fits the terms 1/2x and sin(x). The partial results are then put together using algebra of DNE.

The l'Hospital rule yielded a sequence that does not have a limit. What does it mean? Since the l'Hospital rule applies only if it gives a limit, it follows that its use was not successful and gives no information about the original sequence. So the given sequence may have a limit or not, we do not know.

What can we do? There are two possible approaches. One is to say, fine, if we cannot calculate the answer, perhaps we can guess it using intuitive evaluation. What happens when n gets large? The sine oscillates between −1 and 1, so the term nsin(n) oscillates between values -n and n. This means that it can be ignored compared to n² and we can argue

Very nice, but how do we prove that the sequence indeed converges to 1? One possibility is suggested by the boundedness of sine: The Squeeze theorem (see the box "comparison and oscillation"). In fact, even if we did not do the guessing, we should start thinking of this box, since it is often applied to limits with oscillating terms that cause troubles.

First we have to find some bounds, then we look at the limits of these bounds. If they happen to be the same, we proved the limit.

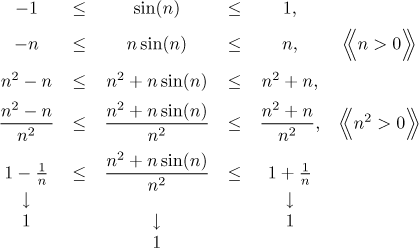
We used the fact that 1/n→1/∞ = 0. Our guess is proved.

We can also try this:

The fraction sin(n)/n converges to zero, which can be proved using the Squeeze theorem similarly as above, but now we can even use its absolute value version, which is easier:

|sin(n)/n| = |sin(n)|/n ≤ 1/n→0.

We will now try some modifications of this problem to see how oscillating expressions behave.

Problem: Find the following limit (if it exists):

Solution: What happens if n goes to infinity? Just like above, the sine part in the numerator is negligible compared to n², so we get

The easiest way to prove it is probably by comparison. Why? Since we guessed that the sequence tends to infinity, we do not really need an upper estimate, it is enough to find a suitable lower estimate to "push the sequence up". Since comparison is easier than squeeze, it is preferable (if it works, that is).

It worked, our guess was proven.

Problem: Find the following limit (if it exists):

Solution: As we argued above, the sine part (that is, nsin(n)) oscillates between -n and n, but now this cannot be ignored compared to the other n in the numerator. Sometimes the sine part is almost n, then the numerator is about 2n and the fraction is 2, and sometimes the sine part is almost -n, then the top is about 0 and the fraction is also 0. So we would guess that the fraction oscillates between 0 and 2. This can be seen better if we cancel:

Now it is clear, the algebra of DNE says "1 + N = N", consequently the given limit does not exist.

Problem: Find the following limit (if it exists):

Solution: What happens here? Just like in the previous example, the numerator oscillates between 0 and 2n; however, since we divide this by n², we would guess that the sequence converges to zero. How do we prove it? Probably the best bet would be comparison again. To save some work we may try the absolute value version of the Squeeze theorem, which has a chance of working because the guessed limit is zero.

Yes, it worked.

We saw very simple problems here, but they represent the major cases one can have. The main message is that when facing some DNE situation, a lot depends on our experience and intuition.

Next problem
Back to Solved Problems - Limits