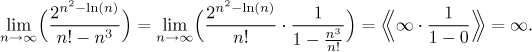Problem: Evaluate the following limit (if it exists)

Solution: We see that we have a ratio of powers, so we would like to use intuitive evaluation; however, there is a little problem in the numerator. If the numerator was just the sum n² − ln(n), we would know what to do; unfortunately, this expression is put into exponential, which means that the intuitive reasoning does not apply any more. What can we do?

In the denominator, we know that when n is really huge, then n³ is negligible compared to the factorial n! and we can ignore it. We also know that ln(n) is negligible compared to n², but since this is happening in the exponent, this is sort of tricky. We know that by ignoring ln(n) we would make just a small mistake for large n, but then we do "2 to the power equal to this small mistake" and we do not know what happens then.

If we do not know what to do, it is usually better to start with an easier problem and then see whether we could use the gained insight in a more complicated situation. So we start by investigating

The scale of powers says "factorials beat exponentials", but that only applies to things like 2ⁿ. We know that multiples in the exponent do not matter, for instance we could argue 2³ⁿ = (2³)ⁿ = 8ⁿ and the factorial would steal beat it, but a square is an altogether different animal. There is no way we can change algebraically 2ⁿ² into something of the form aⁿ.

So we unfortunately conclude that the scale of powers will not give us any answer here. However, it does help somewhat. When the scale was established, the proofs used pairing and comparison. Here we have two things. The factorial n!, which is a product of n elements (numbers 1, 2,..., n), and 2ⁿ², which is a product of n² elements (numbers 2). Could we somehow group these two smartly? We can try this:

How large is this number? Note that all the little fractions are at least one, since 2ⁿ > n. If we apply it to all but the last term, we get

The last fact follows from the scale of powers and can be proved using the l'Hospital rule. We just proved using comparison that the simplified sequence we tried goes to infinity:

Now we sneak in the n³ part and claim that since the factorial prevails over it and so it is negligible, we still have

How would we justify this? There are two possibilities. The traditional way from the box polynomials and ratios with powers is to factor out dominant terms. We get

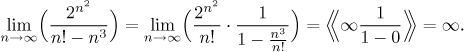
The zero in the evaluation of the denominator follows from the scale of powers, "factorials beat powers." How would we prove it if we needed it? It is done by comparison (factorial cannot be differentiated, so l'Hospital is definitely out, and there is not much other choice).

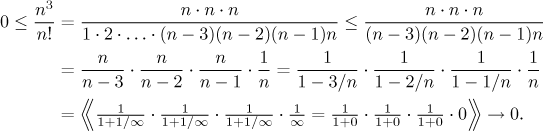
This completes the proof that indeed

Another way to sneak in n³ is to use the approach from the note on intuitive calculations. The idea is as follows: two sequences have the same limit if their ratio converges to 1. So we just compare the two sequences above, with and without n³.

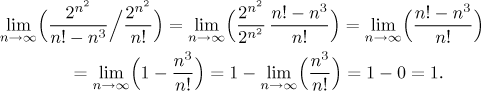
Note that it was very similar to the previous calculation and used the same supplementary fact about the ratio n³/n!.

In fact, there is a much easier way. Since we want to show that this sequence goes to infinity, it is enough to find a suitable lower estimate using the known result. But this is easy, from n! − n³ < n! we get

2ⁿ²/(n! − n³) > 2ⁿ²/n!→∞.

Note that if there were "+" in the denominator, this comparison would not work any more:

2ⁿ²/(n! + n³) < 2ⁿ²/n!→∞.

This says that the sequence on the left has a limit at most infinity (if it exists), but that leaves too much freedom - anything is less than or equal to infinity, the sequence on the left may for instance oscillate (and thus have no limit), or it may go to infinity, just slower than the one on the right, which it actually does! How would we prove it? Easily, the first two proofs that we used would also work with "+" in the denominator.

But enough about this middle step. Now we would like to sneak in ln(n) somehow. Unfortunately, our suspicion above that things are not so easy turns out to be correct when we try it. Namely, could it be true that 2ⁿ² and 2^{n2 − ln(n)} are about the same around infinity? We look at the limit of their ratio and find out that it is not true:

This shows that 2ⁿ² is incomparably larger around infinity than 2^{n2 − ln(n)}. How do we then pass from the latest proven result to the limit we are really looking for? We cannot use what we did so far as a building block:

We got an indeterminate ratio and we cannot apply the l'Hospital rule, since we cannot take derivative of the factorial. Thus algebraically we cannot pass from the known to the given.

How about comparison? We have n² − ln(n) < n², so we can try the following:

Unfortunately, from this type of comparison we cannot make any conclusion. If the given sequence has a limit, it should be less than or equal to infinity (we have to pass to "less than or equal", comparison does not work for sharp inequalities), which means that it can be about anything, including the possibility that it has no limit at all.

So we see that we cannot pass from the known result to the given sequence directly, we have to do it independently of the last known result. Still, since the problems are so similar, perhaps we can gain some inspiration from the work we already did.

One possibility is to use the fact that n is eventually much bigger than ln(n). Note that in the second last calculation we had 2ⁿ² on the top and 2^ln(n) in the denominator, and we know from the scale of powers that the former prevails over the latter. Unfortunately, we have already used up 2ⁿ² to "beat" the factorial in the denominator. However, if you look at the corresponding comparison above, you will see that the inequalities there were very generous, we lost quite a bit in that estimate. Perhaps we do not need all of 2ⁿ² to kill the factorial. Could be "borrow" a piece of 2ⁿ² to also beat the logarithm part? We try it:

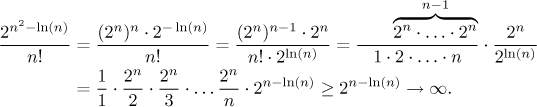
In the last inequality we used the fact that 2ⁿ/2 > 1, 2ⁿ/3 > 1,..., 2ⁿ/n > 1. The conclusion about limit then followed from the fact that n² − ln(n) tends to infinity (see for instance the section on intuitive evaluation) and 2^∞ = ∞. Now the comparison is in the right direction and it follows that

Just like before, there is no trouble sneaking in the n³ part and confirm for instance by factoring that

Next problem
Back to Solved Problems - Limits