Transformations and graph guessing: Survey of methods

Here we will try to make clear how to guess the graphs of functions that were obtained by applying transformations to known functions. We will not cover functions that are obtained by combining more functions together, since guessing such graphs is difficult, often impossible. The situation we cover here is as follows: We have one elementary function and we apply one or more transforms to it. If you already looked at the note on order of evaluation and the algebraic visualization of functions, it will make sense to you when we say that here we will not guess graphs of functions that are not one chain but have more "roots". Incidentally the order of operations may come handy here as well.

An important part of this section will be the list of transformations and how they affect the graph. Since here we are interested in practical application, we will make a "wrong" list in the sense that one transformation will be covered several times, split into special cases. For instance, the scaling cx will be split into four cases, since when working problems, it is intuitively easier. More details on transformations can be found in the section Operations, below we just symbolically express their effect. At the end of this section we will also show how to guess the effect of some functions that do not belong among the traditional transformations, but an experienced student might find the note helpful.

Every transformation works in the same way, by replacing. Every transformation also comes in two flavours, they can be applied to the argument or to the value (that is, to a function). For instance, when scaling by c, we can either replace all x in the formula by c⋅x (scaling the argument), or we can take the formula we currently have and multiply it by c, that is, we replace certain formula f (x) with the formula c⋅f (x). We will represent this replacement procedure by an arrow.

Guessing algorithm
Step 1. Identify the basic elementary function whose graph is the basis for the function you face.
Step 2. Sketch the graph of the basic function, then modify it according to all transforms that are applied to the argument (last to first with respect to the order of operations, see below).
Step 3. Take the graph obtained in Step 2 and modify it according to all transforms that are applied to the value (first to last with respect to the order of operations, see below).

One of the most difficult parts for a student is to recognize the correct order in which the transformations should be applied. Typicaly, there would be two transformations applied to the argument, the question then is which one comes first. Fortunately, there is an easy way to find out. If you start with x and apply the replacements as showed above by arrows in the same order in which you modify the graph, you should get the argument in the given function. If you get something else, your order was wrong. This rule also applies if more transforms are applied.

For instance, when guessing the graph of sin(2x + 3), it is a question whether we should first shift the graph to the left by 3 and then shrink it twice, or first shrink the graph twice and then shift the resulting thing to the left by 3. We will now try the replacement business for both:
Shift first, shrink next corresponds to replacement order         x → (x − 3) → (2x − 3),
in the second step we replace x with 2x.
Shrink first, shift next corresponds to replacement order         x → 2x → 2(x − 3),
in the second step we replace x with (x − 3), so the brackets were necessary.

We see that the first order is correct for the transformation 2x − 3. There is a longer but perhaps a bit more revealing way of showing how the transformations (that is, replacements) affect the starting function. We will show it for the first (correct) variant.

 T   f (x)
    x
x ↦ x − 3:   x − 3
x ↦ 2x: (2x) − 3

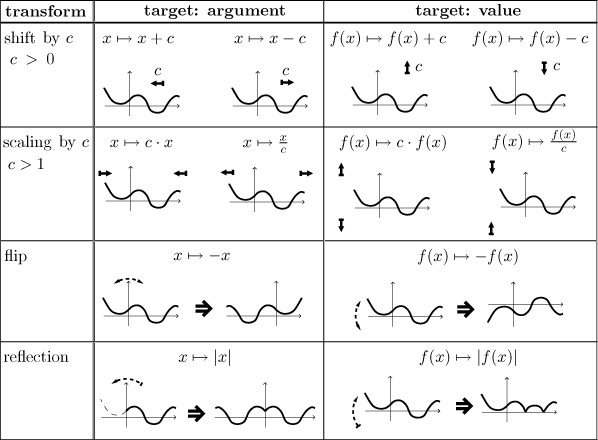
Note: If we think of the order in which we calculate the given expression, the transformations should be applied "last to first". Indeed, if we were to calculate the expression 2x − 3 on a calculator for a particular value x, we would first multiply and then subtract, which fits, since as we saw, the transforms should go in the opposite order. Last to first is a rule you can remember, but only for the argument. Tranformations that apply to values are done in exactly the opposite order, first to last.

Example: Guess the graph of the function

Solution: First we identify the core function. Since transformations do not allow us to divide, we should start with the fraction 1/x. We see a square there which also cannot be done by transformations, so it would seem that the basic function is 1/x2. Indeed, all other operations appearing in f are transformations.

Now we have to apply transformations that change the argument x, we need to change it into (3x − 2), the term inside the square. This means shrinking the graph three times horizontally (towards the origin) and shifting it to the right by 2. Which comes first? If we shrink first, shift next, the replacement chain will go

x → 3x → 3(x − 2).

This does not fit, so we have to do it the other way around, first shift, then shrink.

x → x − 2 → 3x − 2.

Indeed, "− 2" is done last (after "3 times"), so by the rule we should start with it (shift). Thus we do this:

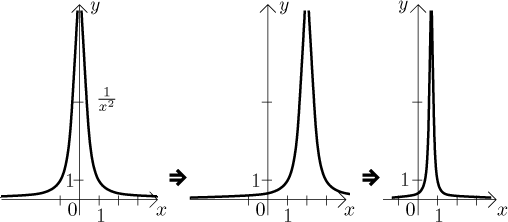
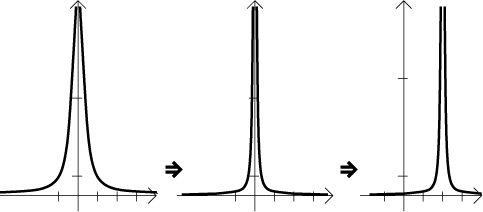
There is sort of a check whether we got it right. The function 1/(3x − 2)2 has a problem (a hole in the domain) at the point 2/3, which seems to fit with our picture, so it might be correct. Note that if we did the two transformations in the wrong order, we would get something different:

In particular, the hole in the domain does not fit.

Now it is time to apply transformations to the value. There are three of them, vertical scaling by 4, shift down by 1 and mirroring using absolute value. The absolute value is calculated last, so it will be also the last one. The "first to last rule" says that we should scale the graph by 4 vertically, then shift down by 1 and then mirror. We check that the replacements work:

We got the right thing at the end, so we do it. First the scaling and shift,

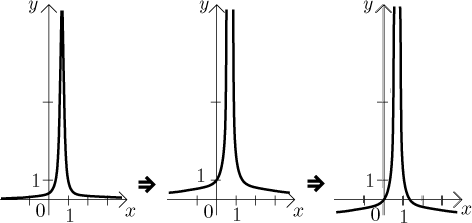
finally the reflection.

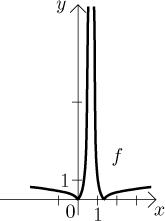
It helps to keep track of some important points during those steps, we may try to substitute zero or check on zero points. Here we just check at the end that the zero points of the given function are x = 0 and x = 4/3, which seems to fit with our picture.

Some other transformations

Here we will cover three more transformations. They are rather advanced and in most calculus courses they do not work with them. We put them here because they are sometimes useful to know (they helped me a few times) and the section would not feel complete without them.

Squaring. Here is the situation: We know the graph of some function f. How does the graph of f 2 look like?

The square power combines two effects. One, it changes all negative values into positive, so we should start by mirroring the negative parts of the graph of f up above the x-axis. The second effect is that of scaling, but unlike the above cases, the scaling is not by a common factor. Briefly, the larger the value of f, the more it gets enlarged by squaring. For instance, in places where f is 10, the graph gets scaled vertically 10-times, at places where f is 1 the squaring does not change it at all, and at places where f is 1/2, squaring will actually halve the height of the graph! This suggests the steps:

1. First, mirror the graph just like when drawing | f |. Then do the following.
2. The points where | f | = 1 and where f = 0 will stay where they are.
3. The points where | f | > 1 will be sent further from the x-axis, that is, the graph will be stretched there vertically; the further | f | is from the x-axis, the more the graph gets stretched there.
4. The points where | f | < 1 will be sent closer to the x-axis, that is, the graph will be squeezed towards the x-axis there; the closer | f | is to the x-axis, the more the graph gets squeezed.

If it is done properly, then the monotonicity of the graph of f 2 must be exactly the same as the monotonicity of | f |. That is, on the intervals where | f | is increasing, the graph of f 2 should be also increasing, and the same is true about intervals of decrease.

Example: On the left we show the graph of some funkce f, we also mark the effect of mirroring and the level 1. On the right, the graph of f 2.

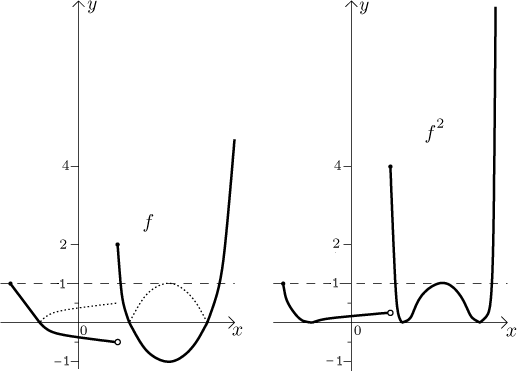
Note: The effect of other integer powers greater than 1 is similar. Even powers work exactly the same, just the stretching and squeezing effect is greater for powers greater than 2. Odd powers greater than 1 have the same stretching/squeezing effect, but without mirroring.

Taking square root. Here is the situation: We know the graph of some function f. How does the graph of the root of f look like?

The square root can be only applied to functions that do not have negative values. Here we have to remember that square root makes numbers larger than 1 smaller, but enlarges numbers smaller than 1. This suggests the steps:


1. The points where f = 1 and where f = 0 will stay where they are.
2. The points where f  > 1 will be sent closer to the x-axis, that is, the graph will be squeezed towards the x-axis there; the further f is from the x-axis, the more the graph gets squeezed.
3. The points where f  < 1 will be sent further from the x-axis, that is, the graph will be stretched there; the closer f is to the x-axis, the more the graph gets stretched.

If it is done properly, then the monotonicity of the graph of f 1/2 must be exactly the same as the monotonicity of f. That is, on the intervals where f is increasing, the graph of f 1/2 should be also increasing, and the same is true about intervals of decrease.

Example: On the left we show the graph of some function f, we also mark the level 1. On the right, the graph of f 1/2.

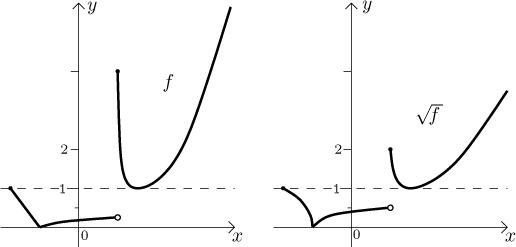
Note: The effect of other roots is similar. If n is an even positive integer, then the n-th root works just like the square root. If n is odd, then the n-th root has similar effect, but now it can be applied to all functions and their negative parts get affected in exactly the same way as we transformed the positive parts.

Taking reciprocals. Here is the situation: We know the graph of some function f. How does the graph of 1/f look like?

The reciprocal can be only applied to functions that are not zero. We know that large numbers are turned into small ones and vice versa by the reciprocal value, but they keep their signs, which suggests what we should do.


1. Divide the graph into horizontal strips. The first strip is the area given by y > 1, that is, it holds the part of the graph were f  > 1. The second strip is the one between levels y = 1 and y = 0. The third strip is between levels y = 0 and y = −1. The last strip is the area below y = −1.
2. The points where f = 1 and f = −1 will stay where they are.
3. The parts of the graph that are in the first two strips exchange places. Points that were close to the level y = 1 stay close. Points that were further will be further in the following way: The pieces of the graph that went to infinity will now approach 0. The parts of the graph that approached 0 will be sent to infinity. It is a sort of flipping around the line y = 1 that must fit into the upper half of the plane.
4. The two strips in the lower half will be treated exactly as in 3., just now everything is and stays negative.

If it is done properly, then the monotonicity of the graph of 1/f must be exactly the opposite of the monotonicity of f. That is, on the intervals where f is increasing, the graph of 1/f should be decreasing, and vice versa.

Example: On the left we show the graph of some function f, we also mark the level 1. On the right, the graph of f −1.

Note: Putting the ideas of 1 - 3 together we now can guess also negative integer powers and roots.

An experienced graph guesser would also know how to handle things like ln( f (x)) or e f (x), but that would be really going too far and we will leave it here.

 

For more examples see Solved problems.

Back to Methods Survey - Basic properties of real functions