Operations with real functions
In this section we will look at different ways of combining functions
together. We start with algebraic operations, then we look at
composition and at the end we briefly survey
transformations of functions. We conclude
this section with a handy notation for
comparison of functions.
Consider two functions, f and g. In order to use
algebraic operations with them (addition, multiplication,...) we first need
to check that they have the same domain. What happens if they do not? Then
there are two possibilities. If their domains are disjoint, then we cannot
put them together algebraically, since the two functions "live" at entirely
different places. Otherwise we just look at the set where their domains
intersect and the result of the operation will have this intersection as its
domain.
Definition (algebraic operations).
Let f,g be functions whose domains are not
disjoint. Then we define the
addition
f + g
by
( f + g)(x) = f (x) + g(x)
for x∈D( f ) ∩ D(g),
subtraction
f − g
by
( f − g)(x) = f (x) − g(x)
for x∈D( f ) ∩ D(g),
multiplication
f⋅g
by
( f⋅g)(x) = f (x)⋅g(x)
for x∈D( f ) ∩ D(g),
division f /g
by
( f /g)(x) = f (x)/g(x)
for x∈D( f ) ∩ D(g) for
which g(x) is not zero.
As a result of these operations we always get a new function, defined on the
intersection as stated above (for division sometimes on a smaller set). The
properties of such a new function are usually some sort of a combination of
properties of the two original functions, but the way they combine depends on
the particular property and on operation, so we prefer to leave this
discussion to parts where the various properties are discussed. One thing
should be noted here, since this property was already covered: the property
of being 1-1 does not get preserved by these operations. If you start with
two functions that are 1-1 and perform one of these operations, you may end
up with a function that is not 1-1.
For example, imagine that we have two 1-1 function f and g
whose values are, among others, f (1) = 1,
f (2) = −1,
g(1) = −1, and
g(2) = 1. How much is
f + g at 1 and 2? We
check:
( f + g)(1) = f (1) + g(1) = 1 − 1 = 0,
( f + g)(2) = f (1) + g(2) = −1 + 1 = 0.
This shows that the function f + g
is not 1-1. Similar
calculations show that also the functions
f⋅g
and f /g are not 1-1, a slight modification of this example would
also show that a difference of two 1-1 functions need not be 1-1.
Since the 1-1 property si not preserved, one also cannot say anything
nice about inverse to outcomes of these operations. There are no nice rules
like
( f + g)−1 = f−1 + g−1,
when it comes to the inverse, an outcome of these operations must be
investigated as a new problem; knowledge of f and g does not
help.
Once we have multiplication of functions, we can also define integer powers
in the usual way, for instance
f 3 = f⋅f⋅f
and
f −2 = 1/( f⋅f ).
This definition can then be extended to rational exponent using roots, and
limit procedure allows us to define
f a for any
real a. Fro details see
Powers in Theory - Elementary
functions.
The last step is to define the general power
f g by
( f g)(x) = e g(x)⋅ln( f (x))
for x∈D( f ) ∩ D(g)
for which f (x) > 0.
For details, see
General powers in Theory -
Elementary functions.
Composition
For the next operation it is useful to recall another visualization of a a
function. The fact that f sends points from one set (a subset of the
real line) to points in another set can be expressed like this:
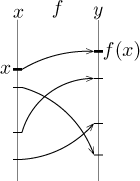
Now the values of the function f are numbers again, so they can be
used as arguments for another function g like this:
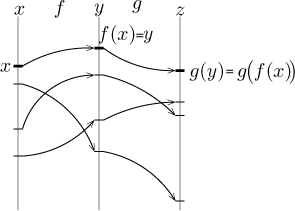
As a whole we get a procedure that sends numbers from one copy of the set of
real numbers (denoted using x) into another copy denoted using
z, we can forget that there was a middle step and consider the whole
thing to be just another function.
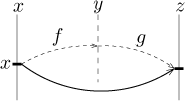
This new function is called the composition of the given two functions
and for this idea to work, one condition is needed: That the values of
f lie in the domain of g (all or at least some). What is the
notation? One is natural. We start with x, then apply f and
obtain the number y = f (x).
To this number we then apply g, thus obtaining
z = g( y) = g( f (x)).
That is, g( f (x)) is the notation for
the composition applied to number x; note that when facing such a composition, we
evaluate from the inside out, that is, we start with x and work
our way out by performing necessary operations. After all, this is not
surprising, when somebody asks you to calculate
(3 + 2)2, you start
by adding 2 and 3, not by squaring (since you do not know what to square
unless you add first). Naturally, f is called the inner
function or inside function, and g is called the
outer function or outside function.
Since x ↦ g( f (x))
gives a prescription for sending
numbers x somewhere, it is in fact another function and deserves a
name. One possible notation is g( f ). Note that when
evaluating functions denoted like this, the inner function is applied first,
so for instance if 2 is a number that can be substituted, then
g( f )(2) = g( f (2)).
To put it another way,
g( f ): x ↦ g( f (x)).
This is one notation for composition, but mathematicians often prefer a
notation of a different kind, since they like to express operations by some
symbol between the two functions involved. Therefore we also use this
notation: g ○ f.
Note that this is read right to left! That is, the
function on the right is applied first and then the function on the left.
Why? So that it fits with the previous notation. One has
(g ○ f )(x) = g( f (x)),
note that the order is the same. Fine, ten points for making sense, but still
it is pretty confusing for many beginners. Beware and be careful.
Example.
Consider the functions
f (x) = x + 2 and
g(x) = x2. How much is
(g ○ f )(1)?
(g ○ f )(1) = g( f (1)) = g(1 + 2) = g(3) = 32 = 9.
How does it work? The number x = 1 is substituted into
f and gives
y = f (1) = 3. Since
g acts on the values of f denoted by y, it may be
instructive to rewrite g as
g( y) = y2. Substituting for
y we now get
z = g(3) = 9.
It is easy to check that (g ○ f )(x) = (x + 2)2
for any x. Note that we used functions whose domains are the whole real line
to avid any troubles with allowable arguments.
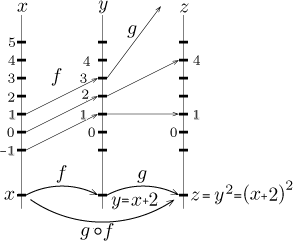
Since there is no trouble with domains, we may also try to change the order
in which we compose these two functions. Since variable names are just for
our convenience, we should not get troubled by the fact that f
"expects" x, but the outcomes of g were called z. We
simply have a new situation, so we can use different letters for variables to
reflect this. This is in fact typical for mathematics. However, there are
situations where variable names have a specific meaning, then it is better to
stick to the given ones (for instance when working with inverse functions, in
applications etc.)
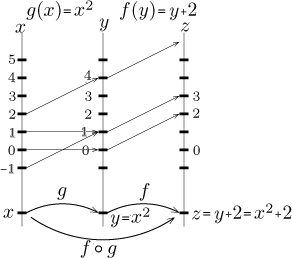
As you can see,
( f ○ g)(x) = f (x2) = x2 + 2.
This shows that composition of functions is definitely not commutative, that
is, f ○ g need not be the same as g ○ f
(and typically it is not).
Now we know how it works, so for the sake of completeness we include a formal
definition.
Definition.
Let f and g be functions such that
R( f ) is not disjoint with
D(g).
We define the composition of f and g as
a function defined for x from the set
D(g ○ f ) = {x∈D( f ); f (x)∈D(g)}
by
(g ○ f )(x) = g( f (x)).
Of course, having more functions, one can compose them like a chain assuming
that their ranges and domains fit:
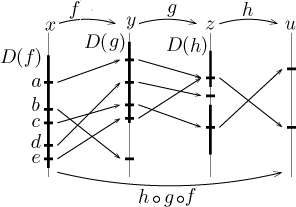
We marked the domains of respective functions. Of the five indicated values
of x, only a, c, and e belong to the domain of
the composition h ○ g ○ f.
Indeed, the number b gets sent by f to
some number f (b) which is not in the domain of g, so
this function cannot be applied to it. The number d was initially
fine, since f (d) belongs to
D(g); thus d
would belong to the domain of the composition
g ○ f.
However, when
g is applied to f (d), the value thus obtained is not in
the domain of h and thus the last step in the composition fails.
To show why this domain fitting is important, consider this example:
Example.
Consider
f (x) = −1 − x2
and g(x) = x1/2 (that is, g is
the square root). We see that the domain of f is the whole real line
(no problem with squaring), its range is the interval
(−∞,−1].
The domain of g
is [0,∞), since we cannot
take the square root of a negative number. Since the range of f does
not intersect the domain of g, we cannot compose them in the order
"f first, then g", that is,
g ○ f.
Indeed, no matter what number x we try, substituting into
(g ○ f )(x ) = (−1 − x2)1/2
we get into trouble. For instance,
(g ○ f )(2)
should be the square root of −5, which does not exist (in the realm of real numbers).
We can, however, compose without problem in the other way, since the range of
g (non-negative numbers) is a subset of the domain of f. We can
calculate
( f ○ g)(x) = f (x1/2) = −1 − (x1/2)2.
This new function has domain
[0,∞)
because of the root. Algebraically, this formula can be simplified
as −1 − x, but one still has to keep in mind that as a result of
composition, this is only considered on the interval
[0,∞). Note that if we were given
this formula as an independent function, not influenced by any background or
past calculations, we would determine the domain of
−1 − x as the whole real line.
Composition behaves nicely with respect to the 1-1 property. If f and
g are both 1-1, then their composition (in any order that makes sense)
is also 1-1 (we will make a formal statement below). If one or both functions
are not 1-1, then nothing can be said about their composition.
Recall that the 1-1 property is closely related to the existence of an
inverse function. Now that we have the notion of composition, we can rewrite
the definition of inverse function. Given a 1-1 function f, its
inverse f−1 is characterized by these equalities:
•
f−1( f (x)) = x
for all x from D( f ),
•
f ( f−1( y)) = y
for all y from R( f ).
In the language of composition, an inverse function is a function that
satisfies
f−1 ○ f = IdD( f )
and f ○ f−1 = IdR( f ),
where IdM is the identity function on a set
M, for further info see
Identity function in
Theory - Elementary functions.
Theorem (composition and inverse).
Let f and g be functions that are 1-1 and
such that the composition g ○ f makes
sense. Then the function
g ○ f
is also 1-1 and its inverse satisfies
(g ○ f )−1 = f−1 ○ g−1.
Note that inverse reverses the order in composition, this is important as we
know that composition is definitely not commutative. The part about
"composition making sense" means that the range of f intersects the
domain of g so that their composition is defined for at least some
values of x. Since the domain and range of an inverse function are the
range and domain of the original function, also the composition of the
inverses will make sense, that is, the range of g−1 will
intersect the domain of f−1.
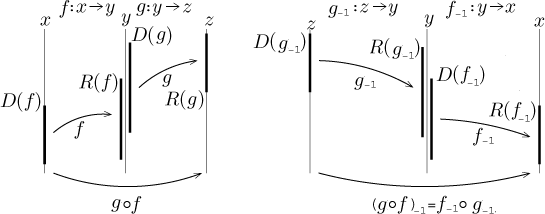
If we tried to compose the inverses in the other way, this is no longer true.
In fact, this is an example where keeping the names of variables is rather
helpful. The original composed function should send x's to z's.
Thus the inverse should send z's to x's. It does work when we
did it the right way above, but fails when we try it the other way; now the
variables do not even match, do not form a chain, which should suggest that
something is wrong here.
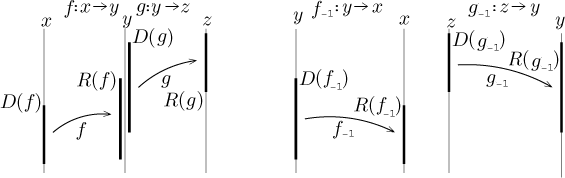
Transformations
Operations with functions have a very interesting special case: When one of
the functions is a constant function. The other function then gets
transformed. Therefore consider a function f (x) and a real
number c.
Case 1:
Define
g(x) = f (x) + c,
or
g = f + c for short. The function g has
all its values shifted by the same amount, so its shape stays the same. The
graph of g can be obtained by shifting the graph of f
up by c if c is positive or down by
|c| if
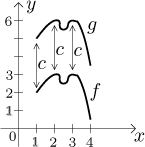
c is negative. In the following picture,
g = f + 3, therefore the graph of g is obtained
by shifting the graph of f up by 3.
Case 2:
Define
g(x) = f (x + c).
The function g has argument increased always by the same amount. If we
think of x as time and imagine that c is positive, then
g at time x is obtained by looking at f at a time
somewhat to the future, which means to the right on the x-axis. In
other words, we obtain the value of g by looking at the graph of
f a bit to the right; thus the graph of g will be just like the
graph of f, but shifted to the left. Similarly, for negative c
we will be looking at f at earlier times. Thus in general for case 2,
the shape stays the same, the graph of g can be obtained by
shifting the graph of f left by c if c is
positive or right by |c| if c is negative. In the
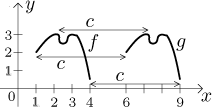
following picture we will show the graph of
g(x) = f (x − 5),
so it will be just the graph of f shifted right by 5.
Case 3:
Define
g(x) = c⋅f (x),
or
g = c⋅f for short. The function
g has all its values multiplied by the same amount. If c > 1,
then at places where g is large, it gets much larger, while at places
where g is small, it gets larger, but only by a little bit. For
instance, if c = 2, then twice a large number is a big
change, while twice almost zero is still almost zero. In the following
picture one has
g(4) = 2⋅f (4) = 2⋅0 = 0,
which means no change at all, whereas
g(2) = 2⋅f (2) = 2⋅3 = 6,
a large change.
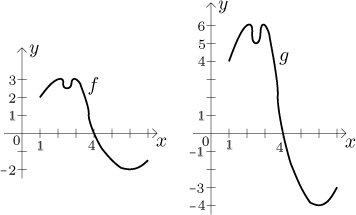
In words, the bigger are the values of f - that is, the further is the
graph of f from the x-axis - the bigger is the change when
going to g = 2⋅f. From this one would guess
that the graph of g can be obtained by stretching
proportionally with respect to the x-axis (that is, by changing the
amplitude). If c > 1, values get larger and the graph expands, if
0 < c < 1, values get smaller and the graph shrinks. If c is
negative, then there is again the expanding/shrinking alternative depending
how |c| compares to 1, but this time the graph also flips around the
x-axis. In the following example we first recall the function f
as above, then show the graph of
g = 2⋅f and
then the graph of g = −1/2⋅f.
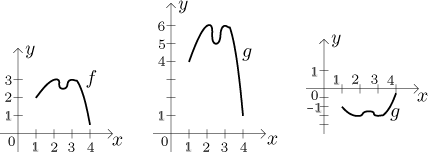
Special case: g = −f has graph equal to the graph of
f flipped symmetrically about the x-axis.
Case 4:
Define
g(x) = f (c⋅x).
To see the effect of this transformation, imagine that you drive on a road and
f is the height of the hills along the road. What does it mean when we
consider
g(x) = f (3⋅x)? To see
g at time x, we look at f at time three times bigger.
That is, this transformation corresponds to making the time go faster, and
when we go faster, the hills seem to come more quickly, as if they were
squeezed closer together. Thus the graph of this g will be the same as
the graph of f but squeezed three times in the horizontal direction
with respect to the origin. Just like the previous case, the further one gets
from the y-axis, the larger the change. If
0 < c < 1, the
time slows down and the graph stretches to go slower. In the following
picture we show
g(x) = f (x/2).
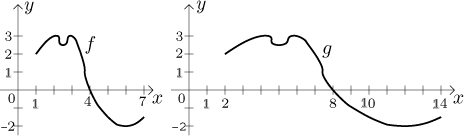
For instance,
g(10) = f (10/2) = f (5) = −3/2.
It sort of makes sense, before it took us 4 hours to get past the 2-hump
hill, with g it takes twice as long.
Therefore, in general, the graph of the function g can be obtained by
stretching the graph of f c times in horizontal
direction, with respect to the y-axis, in case
c > 1, and
shrinking the graph of f 1/c times in horizontal direction,
with respect to the y-axis, in case
0 < c < 1. If c is
negative, the graph is again transformed horizontally depending on whether
|c| is larger or smaller then 1, but now the graph is also flipped
around the y-axis. In the following picture we recall f as
above, then show the graphs of
g = f (2⋅x) and
g = f ((−1/2)⋅x)
(compare to the last example).
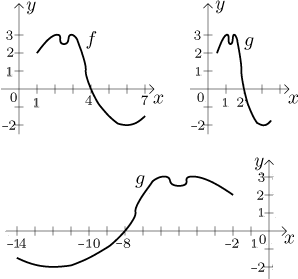
Special case:
g(x) = f (−x) has graph
equal to the graph of f flipped symmetrically about the y-axis.
One can guess graphs of quite complicated functions by knowing the graphs of
elementary functions and applying transformations to them. See
Transformations and graph guessing
in Methods Survey.
In general, it is almost impossible to guess the shape of the graph of
a function created from two functions using algebraic operations. Sometimes
we get lucky, the
easiest case is f + g.
At every relevant x, the value
of g is added to (put on the top of) the value of f. One can
imagine the values of g as bars of appropriate height that are moved
up and down so that their bases fit with the shape of the graph of f.
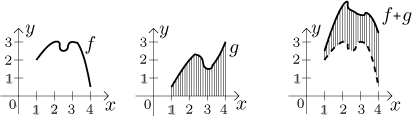
However, this requires quite a bit of experience and imagination and so it is
rarely used.
Short notation, comparison
We already saw an example of a shortened notation,
g = f + c meant
g(x) = f (x) + c
for all x.
In general, when we write an equality or inequality featuring function(s),
but without specifying their argument(s), it is automatically assumed that
this equality/inequality is considered for all possible values of the
argument. Thus
h = f + g means
h(x) = f (x) + g(x)
for all x from the intersection of the domains of the functions f and
g.
Similarly, f ≤ g
means f (x) ≤ g(x)
for all x from the intersection
of the domains of f and g. This is how we compare functions.
There are five possibilities. One can have
f ≤ g
as explained above,
or f < g meaning
f (x) < g(x) for all x from the
intersection of domains; in the other direction there are inequalities
f ≥ g
or
f > g; finally, it can happen that no such comparison is
possible, in other words, for some x the function f is larger,
and for other x the function g is larger.
Basic properties of real functions
Back to Theory - Real
functions