Goniometrické funkce

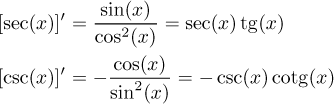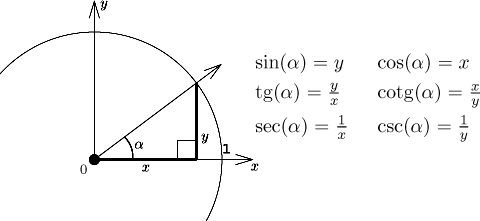
Zde budeme předpokládat, že znáte úhly a jak se měří, mimo jiné že znáte radiány. Pokud si nejste jisti, podívejte se na tuto poznámku.

Existuje několik způsobů, jak definovat goniometrické funkce. Připomeneme stručně dva z nich, založené na geometrické představě. Pak se podíváme na vlastnosti goniometrických funkcí, připomeneme nějaké goniometrické identity, zkusíme zavést inverzní funkce a vše zakončíme stručnou poznámkou o sekansu a kosekansu.

Geometrické definice

Jednotková kružnice. Nechť α je libovolný úhel. Uvažujme jednotkovou kružnici v rovině a paprsek, který jde z počátku pod úhlem α. Nechť (x,y) jsou souřadnice průsečíku paprsku a jednotkové kružnice. Pak definujeme

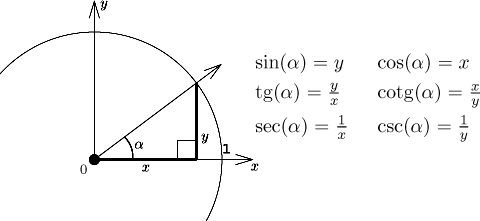
Některé z definic samozřejmě nemají smysl, pokud x = 0, popř. y = 0.

Zřejmě pak máme

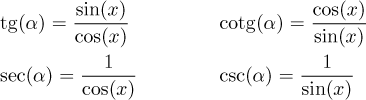
Funkce sec(α) (secans) a csc(α) (kosecans) bývaly velice populární za starých dobrých časů, kdy ještě lidé museli počítat všechno sami, protože docela zjednodušovaly výpočty s goniometrickými funkcemi. Dnes jsou převážně zapomenuty a zahrnujeme je zde, abychom to měli kompletní. Vrátíme se k nim na konci této sekce.

Všimněte si, že když tyto funkce definujeme takovýmto způsobem, pak jsou všechny 2π-periodické, při bližším pohledu jsou tangens a kotangens π-periodické.

Pravoúhlý trojúhelník. Nechť α je nějaký úhel z intervalu (0,π/2). Uvažujme libovolný pravoúhlý trojúhelník s dalším úhlem rovným α. Pak máme následující definice:

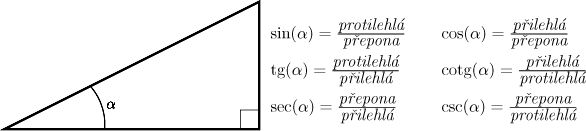
Tyto funkce jsou navzájem propojeny stejnými vzorci jak předtím. Jak tyto definice rozšíříme na libovolný úhel α? Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0.

Pro α z ⟨π/2,π⟩ definujeme sin(α) = sin(π − α) a cos(α) = −cos(π − α).

Pro α z ⟨π,2π⟩ definujeme sin(α) = −sin(α − π) a cos(α) = −cos(2π − α).

Dostaneme tak sinus a kosinus na ⟨0,2π⟩, pak je rozšíříme na všechny úhly opakováním této základní periody. Ostatní funkce se pak definují pomocí sinu, kosinu a oněch vzorců uvedených výše.

Tuto část uzavřeme připomenutím hodnot sinu a kosinu pro populární úhly:

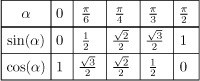
Existuje jednoduchý způsob, jak si je pamatovat pomocí levé ruky.

Další praktická poznámka, namísto zápisu [sin(x)]ⁿ obvykle píšeme sinⁿ(x), podobně pro ostatní goniometrické funkce.

Sinus. Definiční obor:

D(sin) = ℝ.

Graf:

Funkce je spojitá na svém definičním oboru, 2π-periodická, omezená a symetrická, jmenovitě lichá, protože platí sin(−x) = −sin(x). Máme také

sin(x + π) = −sin(x),       sin(x + π/2) = cos(x),       sin(x − π/2) = −cos(x).

Z periodicity máme

sin(x + 2kπ) = sin(x),       sin(x + (2k + 1)π) = −sin(x).

Nulové body sinu jsou body ve tvaru kπ, kde k je libovolné celé číslo; toto jsou také body inflexe. Lokální extrémy jsou v bodech π/2 + kπ.

Co se týče limit v koncových bodech definičního oboru, limita sinu v nekonečnu ani mínus nekonečnu neexistuje.

Derivace:

[sin(x)]′ = cos(x).

Kosinus. Definiční obor:

D(cos) = ℝ.

Graf:

Funkce je spojitá na svém definičním oboru, 2π-periodická, omezená a symetrická, jmenovitě sudá, protože platí cos(−x) = cos(x). Máme také

cos(x + π) = −cos(x),       cos(x + π/2) = −sin(x),       cos(x − π/2) = sin(x).

Z periodicity dostaneme

cos(x + 2kπ) = cos(x),       cos(x + (2k + 1)π) = −cos(x).

Nulové body kosinu jsou body ve tvaru π/2 + kπ, kde k je libovolné celé číslo; jsou to také body inflexe. Lokální extrémy jsou v bodech kπ.

Co se týče limit v koncových bodech definičního oboru, limita kosinu v nekonečnu ani mínus nekonečnu neexistuje.

Derivace:

[cos(x)]′ = −sin(x).

Tangens. Definiční obor:

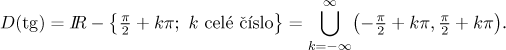
Graf:

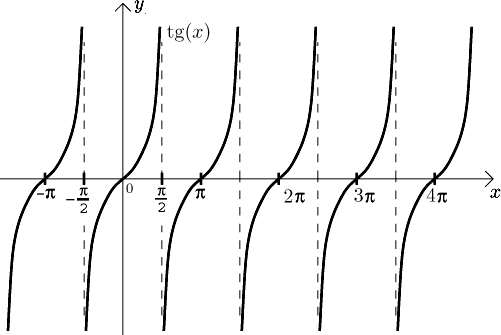
Funkce je spojitá na svém definičním oboru, π-periodická, není omezená a je symetrická, jmenovitě lichá, protože platí tg(−x) = −tg(x). Máme také

tg(x + π) = tg(x),       tg(π − x) = −tg(x).

Nulové body tangensu jsou body ve tvaru kπ, kde k je libovolné celé číslo; jsou to i body inflexe. Lokální extrémy neexistují.

Co se týče limit tangensu v koncových bodech definičního oboru, limita tangensu v nekonečnu a mínus nekonečnu nemá smysl, protože definiční obor neobsahuje žádné okolí nekonečna ani mínus nekonečna. Limity v konečných koncových bodech definičního oboru neexistují, ale máme tam jednostranné limity:

Derivace:

[tg(x)]′ = 1/cos²(x).

Kotangens. Definiční obor:

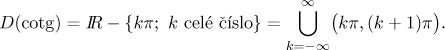
Graf:

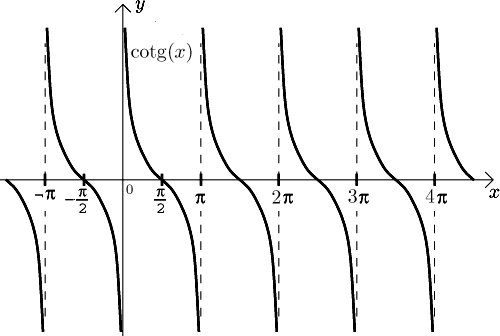
Funkce je spojitá na svém definičním oboru, π-periodická, není omezená a je symetrická, jmenovitě lichá, protože platí cotg(−x) = −cotg(x). Máme také

cotg(x + π) = cotg(x),       cotg(π − x) = −cotg(x).

Nulové body kotangensu jsou body ve tvaru π/2 + kπ, kde k je libovolné celé číslo; jsou to i body inflexe. Nejsou lokální extrémy.

Co se týče limit v koncových bodech definičního oboru, limity kotangensu v nekonečnu a mínus nekonečnu nemají smysl, protože definiční obor neobsahuje žádné okolí nekonečna či mínus nekonečna. Limity v konečných koncových bodech neexistují, ale máme tam jednostranné limity:

Derivace:

[cotg(x)]′ = −1/sin²(x).

Nejprve pár populárních identit pro sinus a kosinus.

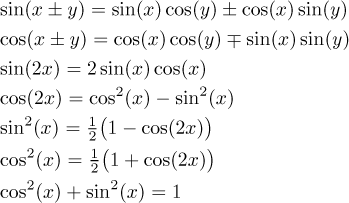
Následující identity jsou méně populární, ale občas velice užitečné.

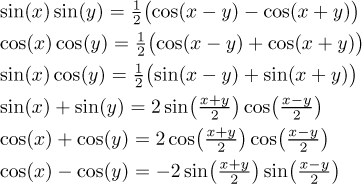
Sinus a kosinus lze dostat (nebo přímo definovat) pomocí exponenciály a komplexních čísel.

A nakonec tento trik, který je také užitečný.

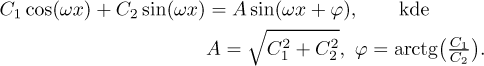
Evidentně máme problém, když C₂ = 0. Pak můžeme brát  φ = π/2  když  C₂ > 0  a  φ = −π/2  když  C₂ < 0.

Teď pár populárních identit pro tangens a kotangens.

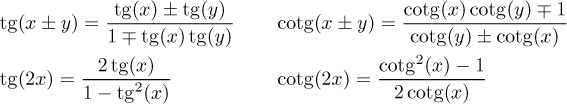
Protože sinus a kosinus jdou vyjádřit pomocí komplexních exponenciál, je totéž pravda i pro tangens a kotangens.

A nakonec pár vzorců, které spojují sinus/kosinus a tangens.

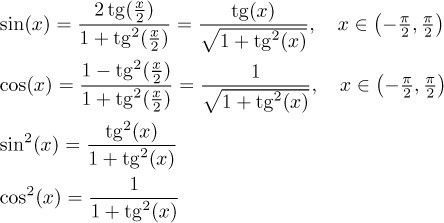
Když se podíváme na grafy nahoře, hned vidíme, že žádná ze základních goniometrických funkcí není prostá, takže nemají inverzní funkce. Na druhou stranu, z praktického hlediska by se nějaká inverze velmi hodila, a lidé také skutečně přiřazovali úhly k velikostem stran trojúhelníku dlouho před tím, než matematici vymysleli pojem inverzní funkce. Abychom to udělali správně, použijeme obvyklý trik, omezíme goniometrické funkce na intervaly, na kterých jsou už prosté. Vybereme intervaly tak, aby byly největší možné (takže pokryjí celý obor hodnot) a také aby dávaly "rozumné" úhly, tedy kolem 0. Je totiž mnohem praktičtější dozvědět se, že nějaký úhel je 30 stupňů, než 750 stupňů (měli bychom správně používat radiány, ale stupně jsou snadnější si představit a hlavně je napsat na Web, tak jsme teď udělali výjimku).

Inverzní goniometrické funkce (cyklometrické funkce). Jsou definovány takto. Nejprve omezíme ony čtyři goniometrické funkce na intervaly dle obrázku.

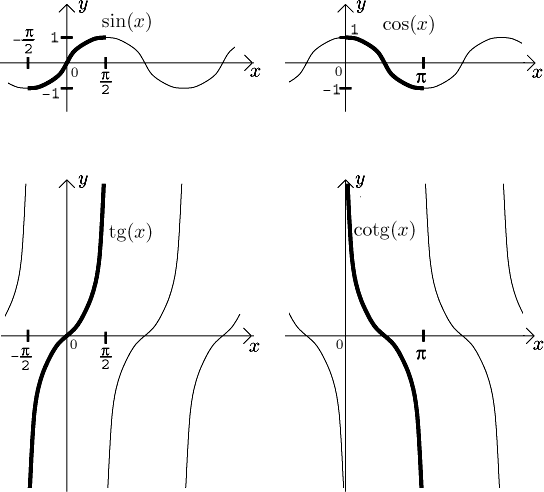
Pak uvažujeme inverzní funkce k těmto restrikcím. Jmenují se arkus sinus (značeno arcsin), arkus kosinus (značeno arccos), arkus tangens (značeno arctg) a arkus kotangens (značeno arccotg).

Grafy těchto funkcí jsou zde:

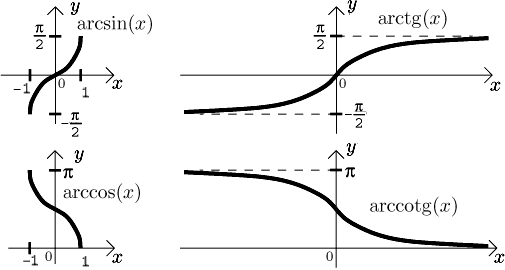
Teď vypíšeme základní vlastnosti těchto cyklometrických funkcí. Jsou všechny spojité, monotonní a omezené.

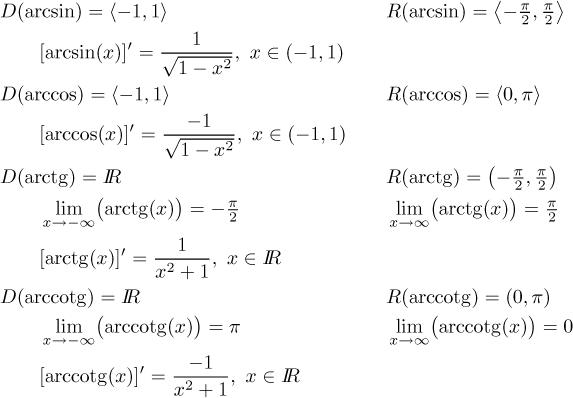
Poznámka: Mnoho autorů (a většina výrobců kalkulaček) používá jiné značení, jmenovitě sin⁻¹(x), cos⁻¹(x) atd. Toto značení je silně matoucí a mnoho studentů cítí (přiznejme si oprávněně) silnou podobnost mezi sin⁻¹(x) a řekněme sin²(x) pro druhou mocninu sinu; logicky pak čekají, že sin⁻¹(x) je vlastně 1/sin(x). Samozřejmě inverzní funkce k sinu a 1/sin(x) jsou dvě zcela rozdílné funkce. Ačkoliv pro toto značení je docela dobré odůvodnění (viz uvedení inverzní funkce v části Teorie - Reálné funkce), je to kvůli těm nedorozuměním velmi nešťastné. Protože máme naprosto správnou alternativu, která je také široce známá - jmenovitě ty arkus věci - budeme je tady důsledně používat.

Poznámka: Vraťme se k původní otázce, je dáno číslo y a my chceme najít x splňující řekněme sin(x) = y. Pokud je toto x z rozmezí, na které jsme před chvílí omezili sinus, pak máme řešení x = arcsin( y). Co když ale z nějakého důvodu potřebujeme x z jiné části reálné osy? Z jiného úhlu pohledu, kdybychom omezili sinus na jiný rozumný interval, jaký by pak byl vzorec pro invezní funkci k takto omezenému sinu? (A samozřejmě i kosinu atd). Platí následující vzorce:

• Nechť sin(x) = y.
  Pokud   2kπ − π/2 ≤ x ≤ 2kπ + π/2   pro nějaké celé číslo k, pak

  x = arcsin( y) + 2kπ.

  Pokud   (2k + 1)π − π/2 ≤ x ≤ (2k + 1)π + π/2   pro nějaké celé číslo k, pak

  x = (2k + 1)π − arcsin( y).

• Nechť cos(x) = y.
  Pokud   2kπ ≤ x ≤ 2kπ + π   pro nějaké celé číslo k, pak

  x = arccos( y) + 2kπ.

  Pokud   (2k + 1)π ≤ x ≤ (2k + 1)π + π   pro nějaké celé číslo k, pak

  x = (2k + 2)π − arccos( y).

• Nechť tg(x) = y.
  Pokud   kπ − π/2 < x < kπ + π/2   pro nějaké celé číslo k, pak

  x = arctg( y) + kπ.

• Nechť cotg(x) = y.
  Pokud   kπ < x < kπ + π   pro nějaké celé číslo k, pak

  x = arccotg( y) + kπ.

Existují velice zajímavé vzorce spojující goniometrické funkce a jejich inverze. Nejsou moc často používané, ale jsou tak pěkné, že se neudržíme a dáme je tu.

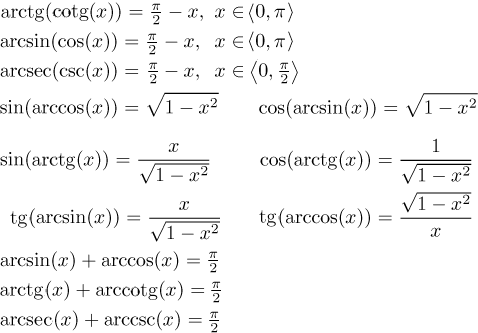
Jen si stručně projdeme jejich vlastnosti. Grafy:

Derivace:

Hyperbolické funkce
Zpět na Teorie - Elementární funkce