Powers as numbers and functions
We start with the following question. We have two real numbers, A and
B, and we want to know how to calculate
AB
(if it is at all possible).
We will define this power step by step depending on the exponent B,
starting from simple ones and going to general ones.
Case 1. B = 0. We define
A0 = 1 for any real number A.
Case 2. B = n is a natural number. We define
An for any real number A by induction,
A1 = A and
An+1 = A⋅An.
That is, An is just
A⋅A⋅...⋅A, the number A
multiplied by itself n-times.
Case 3. B = n is an integer. If n is
not negative, the case is already covered above. If n is negative, we
define
An = 1/An.
In this case A must not be zero.
Case 4.
B = 1/n, where n is a natural
number. It can be proved that if A ≥ 0, then the equation
xn = A has one solution
x ≥ 0. This solution is called the
n-th root of A and we define
A1/n as this root.
Moreover, if n is odd, we can find the root also for negative
A. Thus we can calculate A1/n as the
n-th root for every A if n is odd and for non-negative
A if n is even.
Note: If n is even, there are two solutions to the equation
xn = A, one negative and one
positive. These are solutions to the equation, as a root we only take the
positive one. Some people find this confusing, but it is really quite simple.
The equation x2 = 4 has two
solutions, 2 and −2,
while the square root of 4 is 2.
Case 5. B = p/q is a rational number,
where q is a natural number and p is an integer (we may assume
that p is not zero, since that case was already defined). Now we
define
Ap/q = (A1/q)p,
to determine which A is allowed one has to distinguish several cases.
There are two restrictions:
First, if p is negative, then A cannot be zero. Second, if
q is even, the A cannot be negative. Thus there are four
possibilities:
a) If p is positive and q odd, then A can be any
real number.
b) If p is positive and q even, then we require
A ≥ 0.
c) If p is negative and q odd, then we require
A ≠ 0.
d) If p is negative and q even, then we require
A > 0.
Case 6. B is some real number, again we will assume that it is
not zero. Here we define the power as follows. Choose any sequence
{b(k)} of rational numbers that tends to B (we chose to
write b(k) rather than
bk). Since we
cannot guarantee that all denominators in this sequence are odd, we have to
restrict ourselves to A > 0 if B is negative and to
A ≥ 0
if B is
positive. Then one can show that the sequence
{Ab(k)} converges to some number that we will
call AB.
In order for this definition to be correct, one has to prove three things.
First, that the sequence
{Ab(k)}
really converges. Second, that if we choose a different sequence
{c(k)} going to B, then the sequence
{Ac(k)} converges to the same number
as {Ab(k)}. Finally, one has to
prove that if B happens to belong to one of the above cases (an
integer, a rational number), then the definition via sequences agrees with
the usual definition as in the above cases. Fortunately, all three facts can
be proved and so we have ourselves a power.
The power AB as we defined it satisfies the usual
rules that work whenever the powers involved are defined:
(A⋅B)C =
AC⋅BC,
(A/B)C =
AC/BC,
A−B = 1/AB,
AB+C =
AB⋅AC,
ABC =
(AB)C =
(AC)B.
Powers as functions
Powers as functions come into play when we consider the power
AB and let the base A change, then we
obtain the function
f (x) = xB. We need to know
what it means and see some properties. As before, we will have several cases
depending on what is B. We will start from the most general case, when
B is some real number, and we will see what properties hold for all
powers. Then we will start exploring special cases.
General case: B is a real number.
When we do not have any special information about B, then the domain
is (0,∞). We have the
following properties:
• algebra: For any
x,y > 0 and any real A, B we
have
(x⋅y)B = xB⋅yB,
(x/y)B = xB/yB,
x−B = 1/xB,
xA+B = xA⋅xB.
• comparison: If A < B,
then for any x > 1 we have
xA < xB.
On the other
hand, for x satisfying
0 < x < 1 we have
xA > xB.
• continuity: Powers are always continuous on their domains.
• derivative and integral:
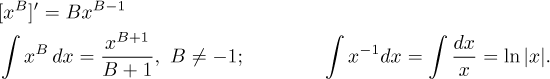
Further properties depend on the sign of B. If
B = 0,
then
xB = x0 = 1,
that is, we have a constant function that is defined on the whole real line.
If B > 0, then the domain of
xB is actually
[0,∞), the function is
bounded from below but not from above (hence also not bounded), it is
increasing. If B < 0, we often prefer to write
xB = 1/xB;
the function is bounded from below but not from above (hence also not bounded),
it is decreasing.
The domain of this function can be extended if we know more about B.
Namely, assume that
B = p/q, where p is
an integer and q is a natural number. Then we can write
xp/q = (x1/q)p,
and we see that such a power actually composition of the
q-th root of
x and the p-th power for p an integer, both functions
are well-known. We will briefly look at them first.
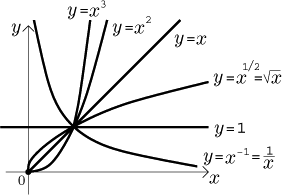
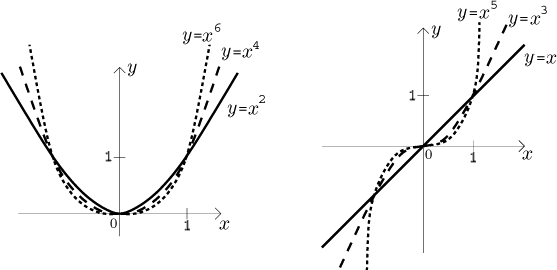
1. Powers xn with n a positive
integer. Their domain is the whole real line. The basic shapes are those of
x, x2 (parabola) and x3. Other
powers have similar shapes, even powers look like x2, odd
powers look like x3, just the graphs are stretched towards
infinity, the higher the n, the more the graph is stretched.
If n is even, then the power
xn is an even function that is bounded from below
but not from above, hence not bounded. If we need a 1-1 part in order to make
na inverse (the corresponding root), we restrict it to the interval
[0,∞). It is increasing on
[0,∞) and decreasing on
(−∞,0].
If n is odd, then power xn is an odd function
that is not bounded from below nor from above (hence also not bounded), it is
1-1 and therefore it has an inverse (the corresponding root). It is also
increasing on the whole real line.
2. For B = 0 we get the constant function
x0 = 1. Its graph is a straight horizontal line. Thus it is
even and bounded, not 1-1 on any interval. It is monotone, namely
non-decreasing and non-increasing.
3. If n is a negative integer, we can write
n = −m, where now m is a natural number, and
xn = 1/xm.
We see
right away that the domain is all real numbers apart from 0. Further
properties follow from what we saw: If m is even, then
1/xm is an even function that is bounded from below
but not from above, hence not bounded. If we need a 1-1 part in order to make
na inverse (the corresponding root), we restrict it to the interval
(0,∞). It is decreasing on
(0,∞) and increasing on
(−∞,0).
If m is odd, then 1/xm is an odd function
that is not bounded from below nor from above (hence also not bounded), it is
1-1 and therefore it has an inverse (the corresponding root). It is also
decreasing on (−∞,0) and
on (0,∞).
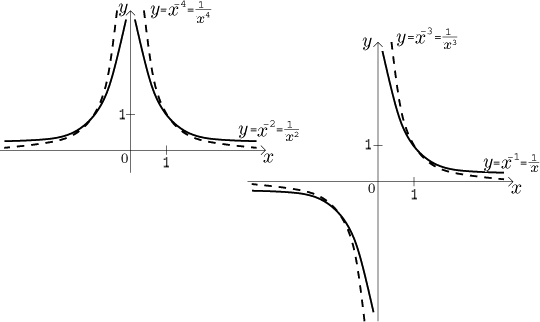
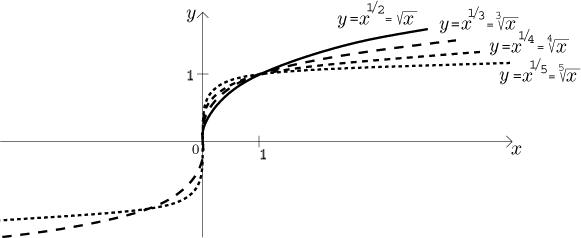
4. If B = 1/n, where n is a natural
number, we define the function x1/n as the
n-th root of x, that is, as the inverse function to
xn. Thus properties of this function follow from the
properties of xn for n a natural number, see
above, in particular they depend on the parity of n.
If n is even, then the domain is [0,∞).
The function is bounded from below but not from above
(hence also not bounded), it is increasing. When n is odd, then the
domain is the whole real line, the function is not bounded, it is odd and
increasing.
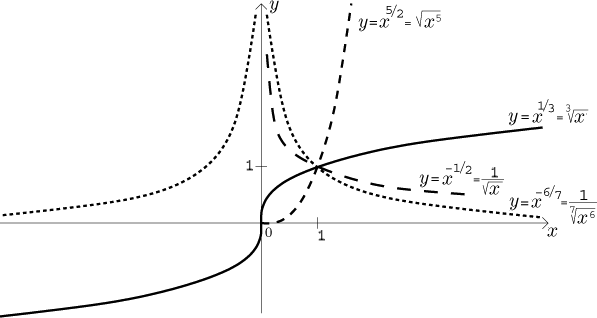
Finally we are getting to the important case of
xp/q = (x1/q)p.
From the analysis above it follows that the behavior of this function depends
on two things, the sign of p and the parity of q.
When p is positive and q even, then the domain is
[0,∞). The function is bounded
from below but not from above (hence also not bounded), it is increasing.
When p is positive and q odd, then the domain is the whole real
line, the function is not bounded, it is odd and increasing. When p is
negative and q even, then the domain is (0,∞).
The function is bounded
from below but not from above (hence also not bounded), it is decreasing.
When p is negative and q odd, then the domain is all
real numbers except from 0, the function is not bounded, it is odd and
decreasing on (−∞,0) and
on (0,∞). In the
following picture, each category is represented by one typical example.
Polynomials, rational functions
Back to Theory - Elementary
functions