Definition.
The hyperbolic sine and hyperbolic cosine are defined
by
![]()
The hyperbolic tangent and hyperbolic cotangent are defined by
![]()
These functions are surprisingly similar to trigonometric functions, although they do not have anything to do with triangles. The similarity follows from the similarity of definitions. At the end of this section we mention another reason why trigonometric and hyperbolic functions might be close.
Definition.
The hyperbolic sine and hyperbolic cosine are defined by
The hyperbolic tangent and hyperbolic cotangent are defined by
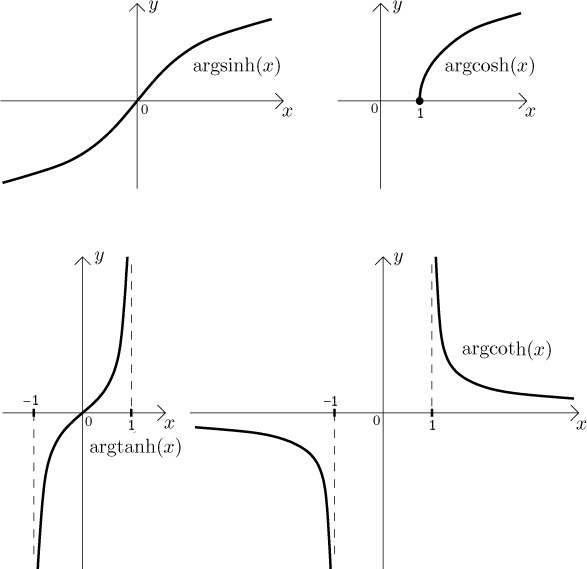
The hyperbolic sine. The domain:
The graph:
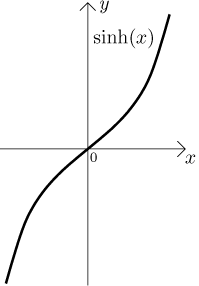
The function is continuous on its domain, unbounded, and symmetric, namely
odd, since we have
There is one zero point, namely
![]()
The derivative:
The hyperbolic cosine. The domain:
The graph:
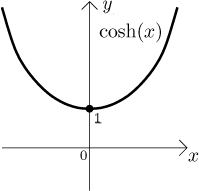
The function is continuous on its domain, bounded from below, and symmetric,
namely even, since we have
There is no zero point, but a local minimum at
![]()
The derivative:
The hyperbolic tangent. The domain:
The graph:
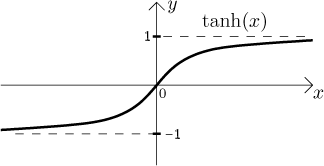
The function is continuous on its domain, bounded, and symmetric,
namely odd, since we have
There is a zero point, namely
![]()
The derivative:
The hyperbolic cotangent. The domain:
The graph:
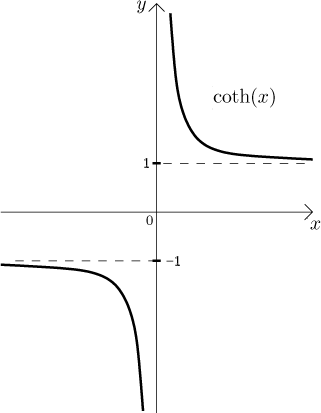
The function is continuous on its domain, unbounded, and symmetric,
namely odd, since we have
There is no zero point and no point of inflection, there are no local extrema. Limits at endpoints of the domain are

The derivative:
Note that we often write
The following identities are very similar to trig identities, but they are tricky, since once in a while a sign is the other way around, which can mislead an unwary student.
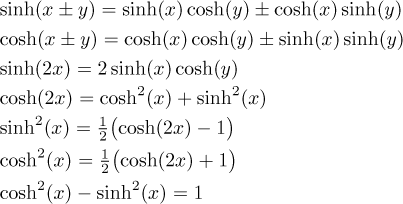
The identities for hyperbolic tangent and cotangent are also similar.
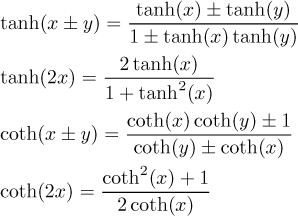
Here the situation is much better than with trig functions. Apart from the
hyperbolic cosine, all other hyperbolic functions are
Basic properties:
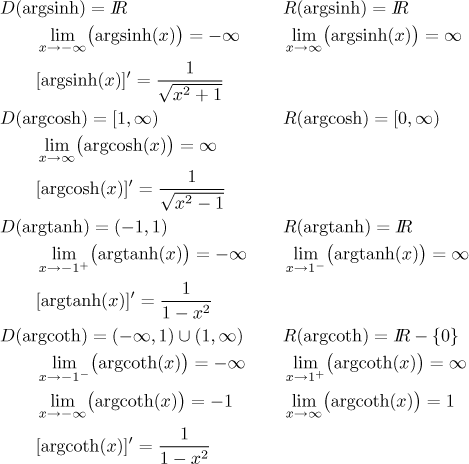
Now we come to another advantage of hyperbolic functions over trigonometric functions. We actually have "nice" formulas for the inverses:
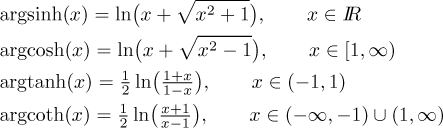
Note: The inverse functions are also sometimes called "area hyperbolic
functions". There are two alternative notations, instead of
One interesting property of trig functions is that they provide a nice
description of a circle. Indeed, the circle of radius r centred at the
origin (given by
What happens if we replace these functions with their hyperbolic cousins? The
equations