Absolute value

Definition.
The absolute value of a real number x, denoted |x|, is defined by

Example: |4| = 4, |1/13| = 1/13, |0| = 0, |−5| = 5 (which is -(−5) indeed), |-0.137| = 0.137.

Note: Normally, when defining a function by cases, the domains of individual cases must be disjoint. Here we put equality with both variants, since when x = 0 they come to the same. In practice one usually takes one inequality with equality and the other sharp, typically the x < 0 one, but it is not necessary.

The graph:

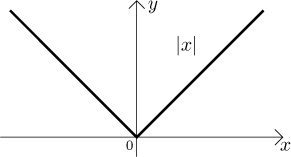
Properties are clear from the picture, the function is continuous, even, decreasing on (−∞,0] and increasing on [0,∞). Concerning the derivative, it cannot be written by one formula, instead we have to distinguish cases:

There is no derivative at 0, but we have one-sided derivatives there, |x|'_-(0) = −1, |x|'₊(0) = 1.

The absolute value is a very popular source of trouble for students, very often they try to take a derivative somehow, arriving at most amazing conclusions. Unfortunately, very little can be done (computationally) with absolute value directly. For most purposes we have to get rid of it by splitting the situation into cases depending on the sign of the expression inside the absolute value (according to the definition) and then work on. If you remember this, you should not run in trouble. For details and examples, see for instance the section on working with split functions in Derivatives - Methods Survey - Graphing functions, and Graphing functions in Derivative - Solved Problems.

Note: There is an alternative way to write the absolute value: |x| = x⋅sign(x). Since the sign function is defined by cases and in investigations we again have to split the situation into more cases, it does not really change things, but this notation may look more friendly, especially since we then get an interesting formula for the derivative: |x|' = sign(x) for non-zero x. This makes it easy to write derivatives of expressions with absolute value, the formulas are cute but they might be misleading in this way, it is important to remember when using such a notation that the derivative does not exist at 0. For more details see the next section.

Sign function
Back to Theory - Elementary functions