Dirichlet function and its modifications

We start with the definition of the Dirichlet function.

Definition.
The Dirichlet function is defined by

Note that both rational numbers (where d = 1) and irrational numbers (where d = 0) are dense in the real line. This means that if we take any open interval, however small, there will be some rational and irrational number in this interval. Intuitively, there are rational and irrational numbers everywhere. Because of this it is impossible to draw the function properly, because we should draw two horizontal lines, but not quite lines:

Since there are rational and irrational points everywhere, these two "lines" have in fact holes in them; these holes are everywhere, there is never even a tiny piece of uninterrputed line. Indeed, concerning the upper "line", every time we take two rational numbers, there will always be some irrational number between them making a hole in the upper "line". Similarly, between every two irrational numbers, however close to each other, there is always some rational, making a hole in the lower "line".

So there are holes everywhere, but these holes are always of single-point size, they never form a bigger hole, for the same reasons as above. For instance, when we take two holes in the upper "line", they correspond to two irrational numbers, and since there is surely some rational number between them, it will make a dot in the upper "line" separating the two holes.

What are the properties of this function? First note that there is not a single point where we would have any one-sided limit. Indeed, pick some number a. In arbitrary neighborhood of a (also one-sided) we find both rational and irrational numbers, so on this neighborhood d oscillates between 0 and 1. Because this oscillation cannot be decreased by making the neighborhood smaller, there is no limit at a, not even one-sided.

Since we do not have limits, we also cannot have continuity (even one-sided), that is, the Dirichlet function is not continuous at a single point. Consequently we do not have derivatives, not even one-sided.

There is also no point where this function would be monotone. Indeed, pick some a, say rational. Then d(a) = 1, and in every neighborhood we have irrationals, where d = 0, both to the right and to the left of a, which rules out any monotonicity. Similar argument works for irrational numbers. Consequently there is no interval where the function is monotone. Similarly one can see that there is no interval where the function is concave up or concave down.

Another interesting property is that d is r-periodic for every positive rational number r. Pick any such r. If x is rational, then x + r is also rational, therefore d(x + r) = 1 = d(x); if x is irrational then x + r is also irrational and d(x + r) = 0 = d(x) as required.

On the other hand, this function is not q-periodic for q irrational. Indeed, 0 is rational, so d(0) = 1, but 0 + q = q is irrational, so d(0 + q) = 0, different from d(0).

In this note we actually prove that this function is not Riemann integrable on any interval.

Modification 1

Define

This function looks like this:

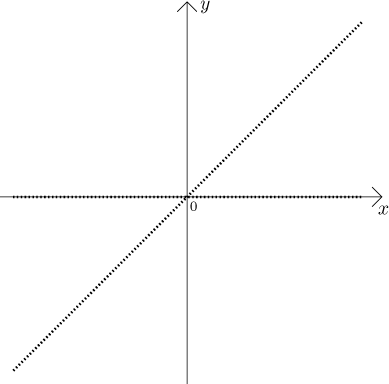
This time we did not draw continuous lines but made them dotted to suggest the scattered nature of the graph, but this one is as misguiding as the previous graph with full lines, because now we have to remember that there are no holes as indicated, what we see as holes is full of dots. Now at rational numbers the dots lie on the line y = x, the irrational dots are still at zero level. This function has a limit at the origin, it is even continuous there, but it is not differentiable there as the slopes in the appropriate limit oscillate between 0 and 1 (details are almost the same as in a similar example in the section on "saw-like" functions).

Modification 2

Define

This function looks like this:

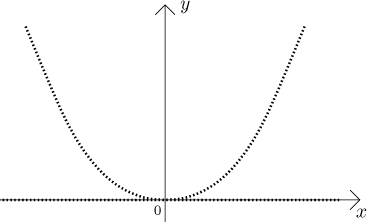
Here the dots corresponding to rational numbers follow the parabola, while the irrational dots are again at zero level. Away from zero, this function is still as bad as the Dirichlet function, but now we even have a derivative at the origin, namely f ′(0) = 0.

This again shows that the existence of derivative at a point does not guaranteee that the function will be nice even on a tiny neighborhood of that point.

Modification 3

Define

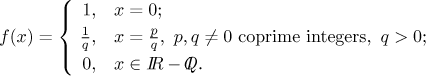
This function is somewhat different. At irrational numbers it is zero, but at other points it is a different story. To imagine it better, we will look at values at various points. To make our task easier, we first show that this function is 1-periodic.

If x is an irrational number, then x + 1 is also irrational, so f (x + 1) = 0 = f (x). If x is rational, then we write it as p/q for coprime integers, as in the definition of the function. Then x + 1 = (p + q)/q with p + q, q coprime, so this is the proper expression and we have f (x + 1) = 1/q = f (x).

Consequently, this function is n-periodic for every positive integer n. But these are the only periods. Just like with the Dirichlet function, irrational numbers are not periods, now also non-integer rational numbers are not periods. Indeed, pick any r = p/q with q > 1, and p, q coprime. Consider x = −r. Then f (x + r) = f (0) = 1, while f (x) = 1/q < 1. Thus r cannot be a period.

Having the periodicity out of the way, we now know that it is enough to know how the graph looks like on [0,1]. We know that at irrational points we get zero, what about other points? We have f (1/2) = 1/2, f (1/3) = f (2/3) = 1/3, f (1/4) = f (3/4) = 1/4, f (1/5) = f (2/5) = f (3/5) = f (4/5) = 1/5. How to imagine this? As we take larger and larger natural numbers n, there are more and more numbers of the form k/n and the dots corresponding to the value of the function at these points go down.

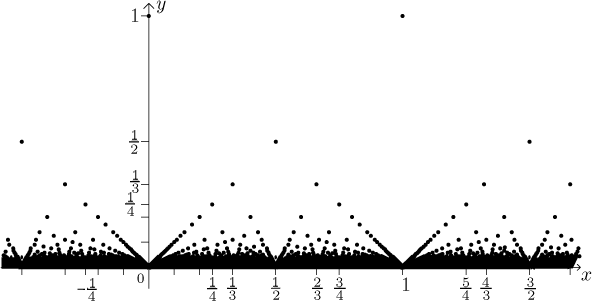
There are more and more points as we look lower, closer to the x-axis, so the graph is quickly becoming quite a mess.

What are the properties of this function? Surprising as it sounds, at every point a we have a limit, namely zero. Since this is the core property of this function and it sounds a bit unbelievable, we will include a proof of this fact at the end as an Appendix.

It follows that this function is continuous exactly at points where it has value 0, therefore f is continuous at all irrational points and discontinuous at rational points. Since we have limits there, we see that these discontinuities are all of the removable kind. This is so weird that we feel it to be the fitting conclusion to our freak zoo.

Appendix

Here we prove that for every a, the function f has limit 0 at a. Indeed, assume that somebody gave us a tolerance ε > 0. We need to find some reduced δ-neighborhood of a so that on this neighborhood, the values of f are within the ε-tolerance from the limit, that is, from zero. This δ is found as follows.

First, find some natural number r so that 1/r < ε. The set of all fractions that lie within 1 from a and whose denominators (in the basic form) do not exceed r is a finite set, therefore there is some δ so that none of these fraction lies within the reduced δ-neighborhood of a. Note that a itself might be one of those fractions, but in the limit we ignore the limit point a itself, so it makes no difference.

Is this δ the right one? Pick any x from this neighborhood. If x is irrational, then f (x) = 0, so surely | f (x)| < ε. If x is rational, then we write it in the basic form as p/q. Since it cannot be one of the fractions that we excluded, we must have q > r, therefore

| f (x)| = 1/q < 1/r < ε.

The proof is complete.

Back to Theory - Elementary functions