Příklad: Najděte (pokud existuje) limitu

Řešení: Je to standardní problém, máme najít limitu výrazu, který existuje na prstencovém okolí limitního bodu. Začneme tedy dosazením tohoto bodu do výrazu.

Sinus nemá v mínus nekonečnu limitu, takže nemůžeme jít dále pomocí algebry limit. Co se dá říct o výrazu ve jmenovateli? Jak se argument sinu blíží k mínus nekonečnu, sinus neustále osciluje mezi −1 a 1. Tato oscilace je násobena číslem jdoucím k nule, takže podle pravidla "omezená krát nula je nula" tvrdíme, že jmenovatel jde k nule. Pro úplnost to dokážeme.

Je to typický příklad ze šuplíku srovnání a oscilace, použijeme srovnávací test. Protože máme vlastní limitu, potřebujeme Větu o sevření, a protože ta limita je nula, je asi lepší verze s absolutní hodnotou.

|x⋅sin(1/x)| = |x|⋅|sin(1/x)| ≤ |x|⋅1 = |x|→0 pro x→0-.

Máme tedy situaci

Jaký typ nuly máme ve jmenovateli? Jak se x blíží k 0 zleva, dosazujeme čísla, která jsou záporná a velmi blízká k nule. Ve jmenovateli pak násobíme x (záporné číslo) sinem 1/x. Potřebujeme tedy znát znaménko toho sinu. Jenže jak se x blíží k 0 zleva, sinus 1/x neustále osciluje mezi −1 a 1, celý výraz tedy bez ustání přeskakuje ze záporného na kladný a zpět, aniž by se usadil na jedné straně.

Toto ukazuje, že nula není jednostranná a celý daný zlomek osciluje mezi kladnými a zápornými čísly, které se velikostí zvětšují pro x jdoucí k 0-. Zhruba řečeno, daný výraz osciluje mezi tendencemi jít do nekonečna a mínus nekonečna.

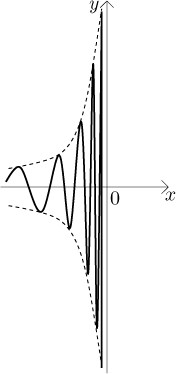
Jakkoliv to podáme, závěr je že daná limita neexistuje.

Poznámka: Co kdyby se po nás chtělo tento závěr dokázat? Asi nejsnažší je použít Heineho větu. Že limita neexistuje dokážeme, když se nám povede najít dvě posloupnosti {xn} a {yn}, které jdou k 0 zleva a když je dosadíme do daného výrazu, dostaneme rozdílné limity. Jednu posloupnost vybereme z bodů, kde je sinus −1, tím "chytíme" dolíky, druhá posloupnost bude z bodů, kde je sinus 1, tím chytíme kopečky.

Nejprve uvažujeme xn = −1/(π/2 + 2nπ). Pak xn→0-. Když tohle dosadíme do dané funkce f, dostaneme

f (xn) = −π/2 + 2nπ→−∞.

Na druhou stranu, uvažujme yn = −1/(3π/2 + 2nπ). Pak yn→0-. Když tohle dosadíme do dané funkce f, dostaneme

f ( yn) = 3π/2 + 2nπ→∞.

Toto dokazuje, že f nemůže mít limitu v 0 zleva.

Další příklad
Zpět na Řešené příklady - Limita