Problem: Evaluate (if they exist) limits of the function

at x = 0 and at infinity.

Solution:
Limit at x = 0.
This is a standard problem, we want to find a limit of an expression that exists on a reduced neighborhood of the limit point. This is not actually all that clear, so we start by rewriting the given function into its proper form, since general powers have to be investigated in the "e to ln" form.

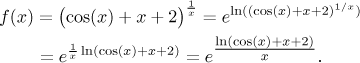
When x is close to 0, for instance if |x| < 1, then cosine is at least 0, so we get cos(x) + x + 2 > 1. Therefore the logarithm exists and so the whole expression exists on the reduced neighborhood of zero (−1,0) ∪ (0,1).

This confirms that the question makes sense and we can start the usual way, substitute 0 into the expression. Since we will be working with the function in the "e to ln" form and the exponential can be pulled out of the limit, we will just focus on the expression inside the exponential for a while.

Dividing a non-zero number by zero is an indeterminate expression, unless we can force the zero in the denominator to be one-sided. There does not seem to be any reason for this here, which makes us suspicious, perhaps the limit does not exist. To make sure, we use the standard trick and look at one-sided limits:

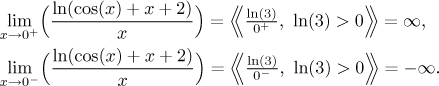
Since the one-sided limits do not agree, the given (two-sided) limit does not exist. Note that we had to inquire about the value of ln(3), since if ln(3) were negative, the infinities would be the other way around, and if it were zero, we would have an indeterminate ratio and a different approach would be needed.

Now we would like to claim that if we are raising e to an expression that does not have a limit, we obtain something that does not have a limit. If fact, in this particular case it is true, but it is not immediately clear and it is definitely not a rule that would work for all (even nice) functions. Thus to make sure and show a proper solution we look at one-sided limits of the given function f itself, of course we will use the above calculations.

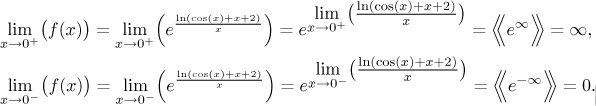
This confirms that the limit of f at x = 0 does not exist.

Limit at infinity.
From cos(x) + x + 2 > x we see that in fact the logarithm in the expression above exists for all positive x, thus the function is defined on a neighborhood of infinity and the limit there makes sense. As usual, we start by substituting infinity into the given expression.

Is this an indeterminate expression? This is not immediately clear. One can actually show that the numerator goes to infinity (see below), but we do not really need it, since we have the wonderful more general form of l'Hospital's rule that will now save our time.

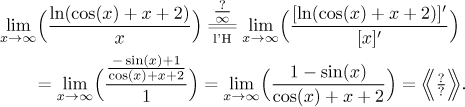
What can we say about the expressions in the fraction? In the numerator we have an oscillating but bounded expression, it keeps oscillating between 0 and 2. In the denominator, the cosine - a bounded function - is added to the expression "x + 2" that goes to infinity at infinity. The rule "bounded plus infinity is infinity" comes to mind here. Just to be sure, we will prove this conclusion, the easiest way seems to be the comparison test. Indeed, for x > 0 we have

cos(x) + x + 2 ≥ (-1) + x + 2 = x + 1→∞ at infinity.

This confirms that the expression in the denominator goes to infinity, now we could use the rule "bounded divided by infinity is zero." For the sake of completeness we will actually prove this conclusion, this time we will have to use two-sided comparison, that is, the Squeeze theorem:

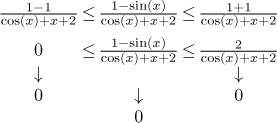
Thus we confirmed that the expression goes to zero at infinity. Now we have to remember that we are not really interested in this particular expression, but in "e to this expression". Therefore we have to return back to the given function.

Next problem
Back to Solved Problems - Limits