Problem: Evaluate (if it exists) the limit

Solution: This is a standard problem, we want to find a limit at negative infinity of an expression that exists on a neighborhood negative infinity (e.g.\ for x < 0). Thus we start by substituting negative infinity into this expression.

We obtained an indeterminate ratio, what will be the best way to handle this problem? One possibility is to try the l'Hospital rule.

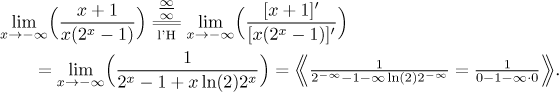
We have an indeterminate product in the denominator. The standard approach is to change it into a ratio and then most likely apply the l'Hospital rule to this ratio, but for that to work we have to get rid of the remaining parts of the expression (l'Hospital's rule can only be applied to fractions, not to fractions inside something). The easiest thing is to simply look at the offending product x2^x directly as an individual problem. Once we decided on this, we have to make another decision regarding which part of this product we will "put under". Normally we would put under the x, since by changing it into x⁻¹ we do not increase the difficulty considerably. However, here this is not so good.

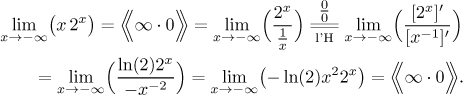
As you can see, the problem is that the exponential 2^x gets preserved by the derivative, so we are in trouble. We try it the other way:

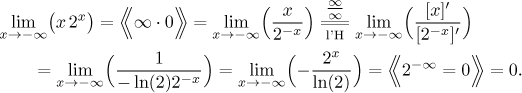
Now we know how the product behaves and we are ready to complete the problem.

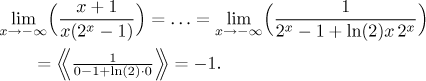
Is there an easier way? There are two possible alternative approaches. Both stem from the observation that the given expression is a ratio of powers and exponentials, which is something that we know quite well, but we have a little problem: the scale of powers and intuitive calculations only works at infinity, but here we have negative infinity.

The first possibility that we see is to change negative infinity into infinity using substitution.

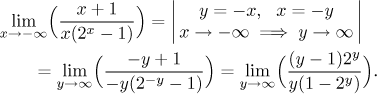
Now it is a typical expression with powers and exponentials whose limit at infinity can be guessed. When y is really huge, then y − 1 behaves like y and 1 − 2^y behaves like −2^y, so we get

Thus we would guess that the limit should be −1, which can be confirmed by factoring out dominant terms. The intuitive calculation showed that the dominant term in both the numerator and the denominator is y2^y.

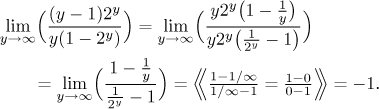
Thus changing negative infinity into infinity via substitution really did help.

What is the other alternative? The usual guessing works at negative infinity for powers (and also polynomials). This suggests that we could use this intuitive evaluation approach only for a part of the given expression, namely those polynomials, and do the part with 2^x separately, especially since we notice that it did not cause any trouble when we substituted negative infinity at the beginning.

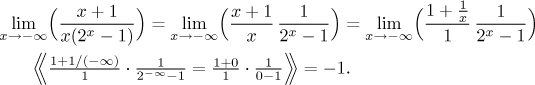
This was definitely the simplest solution.

There is a moral to this story. When we have an expression which has parts of different types, it often helps to separate parts of different kind and put them together according to type (if it is possible). Often, when we put parts of similar type together, we get a chance to simplify. In our example it paid off to put together powers on the one hand and exponentials on the other hand (well, there was just one, but the idea is clear). This approach can also help with other kinds of problems, not just limits.

Next problem
Back to Solved Problems - Limits