Problem: Evaluate (if it exists) the limit
![]()
Solution: This is a standard problem, we want to find a limit at infinity of an expression that exists on a neighborhood of infinity (e.g. for x > −1), thus we start by substituting infinity into the expression.
![]()
We should start by tackling the indeterminate fraction, but this one is actually simple. Since it is a ratio of polynomials at infinity, we can use the tricks from intuitive evaluation to guess the answer:
![]()
This answer can be confirmed by factoring out, but there is no need to hurry,
since this would give us information only about the second part of the given
expression. Now we know that as a whole it is an
indeterminate product
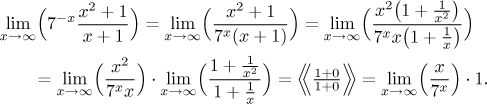
The fraction at the end is of the type "infinity over infinity" and it is a textbook example for the l'Hospital rule.
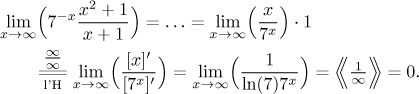
This was probably the optimal solution. Are there any alternatives? One possibility is to look at the fraction that we get after moving 7x into the denominator. This is an indeterminate ratio that features "nice" functions, so l'Hospital's rule might help here.
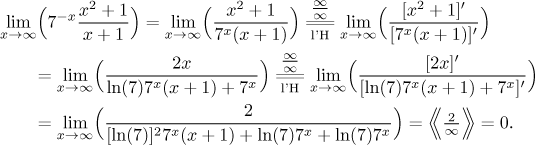
Well, probably not as nice as the first solution but still manageable.
The third possibility that comes to mind is this: At the beginning we found out that the fraction goes to infinity and therefore we had an indeterminate product. The standard approach is to "put under" some nice part, here most likely the exponential 7x, and then apply l'Hospital's rule.
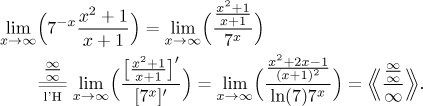
Things got worse rather than better it seems, so this way is not as good. How
would we go on if we did not have the better solutions above? The fraction in
the numerator goes to 1 (dominant terms on the top and bottom are both
x2), so the whole fraction is