Problem: Evaluate (if it exists) the limit

Solution: We have a general power, so we should start by rewriting it into the canonical "e to ln" form.

This function exists on (0,∞), which is a right reduced neighborhood of the limit point x = 0. Thus we start by substituting this point into the expression.

This is an indeterminate power, the standard approach calls for changing it into the canonical form as above, pull the exponential out of the limit and what is left is a limit of the type 0⋅∞. This is an indeterminate product.

The standard approach is to change the product into a ratio by putting one part "under". Which part we choose is very important, but here we do not have a clearcut candidate. Both functions become significantly more complicated when "put under", since they become composed with the power to −1. Since we will then be using l'Hospital's rule, we have to think about differentiating, and when we differentiate sin⁻¹ or ln⁻¹, we have to use the chain rule and thus the core function (sine, logarithm) survives. Thus we see that no matter what we "put under", it will become more complicated later on.

Thus we might get some help from a consideration that is usually secondary. When we put one part "under", the other one stays on the top of the resulting fraction and it will get differentiated during the l'Hospital step. Is there any difference here? The derivative of sine is cosine, which is no marked improvement. However, logarithm disappears when differentiated, so this suggests that we will probably want to leave the logarithm on the top.

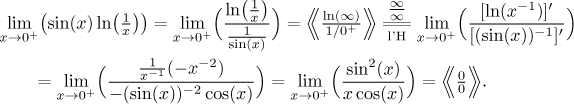
As we hoped, the situation improved. By the way, note how we switched between 1/x (when we wanted to evaluate) and x⁻¹ (when we want to differentiate); such little tricks can help quite a bit. Now we have an indeterminate ratio that looks quite nice, so we try another l'Hospital's rule. Note that the cosine does not cause troubles, so it is a good idea to move it away before we do the l'Hospitaling business.

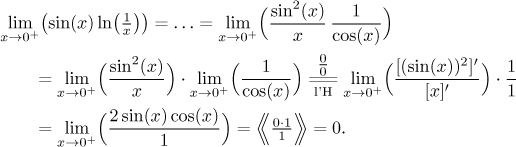
Now we have to remember that we were given a different function, so we have to return to the exponential.

Remarks: Let's take it from the end.
1. It was not really necessary to remove the cosine before l'Hospitaling.

So this way it also was nice, we did not save much trouble above.

2. What if we made the other choice when changing the product into a ratio?

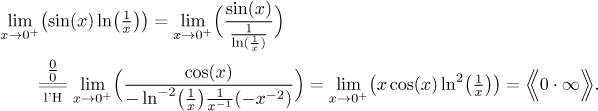
As expected, the situation did not get any better.

3. We can do a little trick at the very beginning that will make all subsequent calculations a bit easier.

The change into ratio and l'Hospital then go like this:

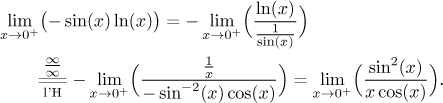
In the end we got to the same expression as above, but the road there was easier.

Next problem
Back to Solved Problems - Limits