Problem: Evaluate (if it exists) the limit

Solution: This is a standard problem, we want to find a limit of an expression that exists on a reduced neighborhood of the limit point. Thus we start by substituting this point into the expression.

Sine does not have a limit at negative infinity, so we cannot continue using limit algebra. What can be said about the expression in the denominator? As the argument of the sine goes to negative infinity, the sine keeps oscillating between −1 and 1. This oscillation is multiplied by a number going to zero, so by the rule "bounded times zero is zero" we claim that the denominator goes to zero. For the sake of completeness we will prove this claim.

This is a typical problem from the box comparison and oscillation, we will use some comparison test. Since we have a proper limit, we need the Squeeze theorem, and since the limit is zero, the absolute value version is probably better:

|x⋅sin(1/x)| = |x|⋅|sin(1/x)| ≤ |x|⋅1 = |x|→0 as x→0^-.

Thus we have the situation

What kind of a zero do we have in the denominator? As x approaches 0 from the left, we are substituting numbers that are negative and very close to zero. In the denominator we then multiply x (a negative number) by sine of 1/x. Thus we need to know the sign of the sine. However, as x goes to 0 from the left, the sine of 1/x keeps oscillating between −1 and 1, thus the whole expression x⋅sin(1/x) keeps switching from negative to positive and back without ever settling down on one side.

This shows that the zero is not one-sided and the whole given fraction oscillates between positive and negative numbers that increase in magnitude as x goes to 0^-. Roughly, the given expression oscillates between going to infinity and negative infinity.

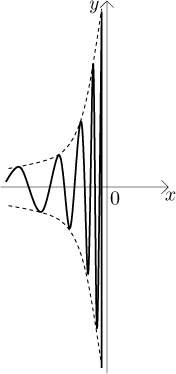
Any way we put it, the conclusion is that the given limit does not exist.

Remark: What if we were asked to prove our conclusion? Probably the easiest way is to use the Heine theorem. We can prove that the limit does not exist by finding two sequences, {x_n} a {y_n}, that go to 0 from the left and when we substitute them to the given expression, we get different limits. One form one out of points where the sine is −1 to catch the dips of the function, the other sequence will be points where sine is 1 to give the hills.

First, consider x_n = −1/(π/2 + 2nπ). Then x_n→0^-. When we substitute this into the given function f, we get

f (x_n) = −π/2 + 2nπ→−∞.

On the other hand, consider y_n = −1/(3π/2 + 2nπ). Then y_n→0^-. When we substitute this into the given function f, we get

f ( y_n) = 3π/2 + 2nπ→∞.

This proves that f cannot have a limit at 0 from the left.

Next problem
Back to Solved Problems - Limits