Basic properties, evaluating limits

We start by looking at a few basic properties of limits. Then we look at theorems used in evaluating limits. This leads directly to the limit algebra, our main tool for evaluating limits. Another topic it leads to is one-sided results of limits, an important ingredient. At the end of this section we will look at connections between the limit and some properties: boundedness, monotonicity, sequences etc.

A few simple statements

The following statements should be clear if you understand what limit means. In all these statements, a can be a real number or (negative) infinity.

Fact.
Let f be defined on some reduced neighborhood of a. Then f converges to L at a if and only if ( f − L) converges to 0 at a.

Fact.
Let f be defined on some reduced neighborhood of a. If f goes to L at a, then | f | goes to |L| at a.

Fact.
Let f be defined on some reduced neighborhood of a. Then f goes to 0 at a if and only if | f | goes to 0 at a.

Fact.
Let f and g be defined on some reduced neighborhood of a. Assume that both converge at a. Their limit at a is the same if and only if f − g goes to 0 at a.

Note that the last statement is not true any more if we drop the assumption about convegence. As usual, all these statements are also true for one-sided limits. This is also true for the following theorem:

Fact.
If f has a non-zero limit at a, then there exists a reduced neighborhood U of a and a constant k > 0 such that | f | > k on U.

For details see separation from 0 in Continuity in Functions - Theory - Real functions.

When we evaluate limits, we always have to start from something that we know. The first source of such limits is this theorem, in fact just a reformulation of a theorem we had before.

Theorem (limit and continuity).
Let f be a function defined on a neighborhood of some real number a. If f is continuous at a, then

The same is true for one-sided limit and one-sided continuity, there we just need existence of f on a one-sided neighborhood. This theorem is quite useful, since we know that all elementary functions are continuous on their domains and so are functions obtained from elementary functions using algebraic operations.

Example: The limit of  f (x) = x² − 3 at a = 4 is f (4) = 13.

Example: We look at the limit at 2 of

The theorem as such does not help here, since g is not given by some obviously continuous function on any neighborhood of 2. However, it is given by x² on some left neighborhood of 2, therefore we can find the limit of g at 2 from the left by substituting x = 2 into this formula. We obtain

g(2^-) = 2² = 4.

What about the limit from the right? The function g is not given by any obvious continuous function on a right neighborhood of 2, so this won't be so easy. Only at the first sight, though. Note that the function h(x) = 2x is defined and continuous on the whole real line, so it has limit at 2 equal to 2⋅2 = 4. Moreover, this function agrees with g on (2,∞), which is a reduced right neighborhood of 2. Therefore the limit at 2 from the right of g is equal to the limit at 2 from the right of h, which is 4.

g(2⁺) = 4.

Since the limit of g at 2 from the left and the limit from the right exist and agree, it follows that g has a limit at 2 equal to 4.

We see that the theorem can be also applied in more general situations, we can obtain a limit of a function f at a by substituting into some expression assuming that this expression by itself is a continuous function at a and is equal to f on some reduced neighborhood of a. An analogous statement is true for one-sided limits.

We know that any expression we create using elementary functions and algebraic operations plus composition is continuous on its domain, and we can recognize whether a lies in this domain simply by trying to substitute a into this expression. From this we get the following rule.

Basic rule for evaluating limits at proper points.
Assume that a function f is defined by some expression on some reduced neighborhood of a real number a. If we substitute a into this expression and it makes sense, then the outcome is the limit of f at a.

Appropriate rules are true also for one-sided limits. There f needs to be defined by a suitable expression on some one-sided reduced neighborhood of a.

Note one trivial case: When we substitute any a into a constant, we get this constant. We also saw in the example above how we can use this rule even if a function is not given by one formula, but by different formulas on each side of a. We then pass to one-sided limits and compare outcomes. This comes handy especially when we work with split functions.

This rule is very useful; however, it would be too easy. In most examples something goes wrong. What can go wrong? If f is not defined by some nice formula on a (one-sided) reduced neighborhood of a, then (unless f is some weird function) the function is not defined on a reduced neighborhood of a and the limit does not make sense. Thus the only interesting case is when f is defined by some expression on a reduced neighborhood of a, but a itself causes trouble when we substitute it into this expression. In other words, a is exactly at the boundary of the domain of this expression.

This situation can be also extended to cases when a is improper, we can consider an expression that is defined on a neighborhood of infinity and we ask for a limit at infinity, similarly for negative infinity. What can we do then?

Some cases are simple. For all elementary functions we know what happens at the endpoints of the intervals of their domains. For instance, we know that the limit of ln(x) at a = 0 from the right is −∞. We can write it for short as ln(0⁺) = −∞. Similarly we can write e^−∞ = 0, or tan((π/2)^-) = ∞. For a concise list, see limit algebra.

It gets more interesting when we start putting such functions together. We need to know how to put information about limits of simple terms together.

Theorem (limit and algebraic operations).
Let a be a real number, ∞, or −∞. Let f,g be functions defined on some reduced neighborhood of a. Assume that f has limit A at a and g has limit B at a. Then the following is true:
(i) For any real number c, the function (c⋅f ) has limit c⋅A at a if it makes sense.
(ii) The function ( f + g) has limit A + B at a if it makes sense.
(iii) The function ( f − g) has limit A − B at a if it makes sense.
(iv) The function ( f⋅g) has limit A⋅B at a if it makes sense.
(v) The function ( f /g) has limit A/B at a if it makes sense.
(vi) The function f ^g has limit A^B at a if it makes sense.

Now what is that remark about making sense? If A and B are real numbers, that is, if the two given limits are convergent, then the operations (i) through (iv) always make sense. However, the ratio A/B only makes sense if B is not zero. And this is exactly what is meant. What we really have here is an extension of the usual algebra. Before, when we wrote "3 + 2 = 5", we meant that three apples added to two apples give five apples. But now it can also mean that "a sequence converging to 3 when added to another sequence that happens to converge to 2 will yield a sequence that converges to 5". This is the "limit algebra" and unlike the usual algebra, this one also features infinities.

We could present a theorem now with many statements, but it is much easier to start from another end. Note that in the theorem above we did not assume that A,B are finite, and some operations can be defined also for cases when they feature infinity. If we use these operation in the above theorem and deem that they "make sense", then all the results we obtain in this way are correct. What operations can we introduce?

If for instance (close to a) f is immensely huge and g is about 1, then f − g gives still immensely huge numbers (a billionaire who drops a dollar is still a billionaire). We just "argued" that ∞ + L = ∞ for real numbers L.
What do we get if we add or multiply two immensely huge numbers? Another immensely huge number. We just argued that ∞ + ∞ = ∞ and ∞⋅∞ = ∞.

On the other hand, we do not know what ∞ − ∞ is, since by subtracting two huge numbers we can get anything. Such expressions are called indeterminate expressions and you will find more information about them in this note. The answers to them may range from limit not existing to improper limit to proper limit, they have to be handled individually.

This shows that the "making sense" for working with limits is different from making sense for numbers. The reason is that now the numbers A,B do not represent real numbers, that is, fixed quantities, but outcomes of limits, in other words, they represent processes, "almost numbers". This has the effect that some operations, although they can be performed with real numbers, do not work with limits. The best example is the power 0⁰. We know that as a number it makes sense, it gives 1. However, if these zeros represent limits of functions, then we are in a situation that we look for a limit of the general power f ^g. When we get close to a, then both f and g are close to 0, but a small number raised to a small number need not be close to 1, it might be very small or very huge, depending on which "almost zero" is closer to zero.

After all, in "normal" algebra we have 0^g = 0 for (small) positive g, whereas f ⁰ = 1 for small positive f. When we send f and g to zero, which of the two results wins? The outcome of the limit (that is, of the expression 0⁰ in the limit algebra) depends on how fast go f and g to 0, the limit might not even exist. 0⁰ is thus an indeterminate expression.

To summarize, the algebra of limits allows us to calculate more complicated limits using the basic limits, we just need to remember what works, what surely does not work, and then there are indeterminate expressions that must be handled individually. You will find more details in the note on limit algebra, we also offer a brief list.

We still did not cover one important operation, that of composition.

Theorem (limit and composition).
Let a be a real number, ∞, or −∞. Let f be a function defined on some reduced neighborhood of a, assume that f has limit A at a. Let g be a function defined on some reduced neighborhood of A, assume that g has limit B at A. If at least one of the following two conditions is satisfied:
1. g is continuous at A, or
2. there is a reduced neighborhood of a on which f ≠ A,
then the limit of g( f ) at a is B.

This theorem is a bit technical, but for practical considerations we may simply remember that if f goes to A at a and g is continuous (which most functions that we meet are), we get the limit of g( f ) simply as g(A).

Example: We know that f = x² − 2x tends to 0 at a = 2. We also know that g = cos(x) is continuous everywhere. Consequently the function g( f ) = cos(x² − 2x) tends to cos(0) = 1 at a = 2.

This in fact nicely fits with the "substitute and see" concept. The two theorems on limits and the limit algebra with infinities allow us to extend the basic rule for evaluating limits to all cases:

If we want to find a limit at a (which now can be also improper) of some expression defined on a reduced neighborhood of a, then we "substitute" a into this expression and if the answer (obtained using the limit algebra) makes sense (it might also be improper), then the outcome is the answer to the limit.

We put "substitute" into quotation marks, since infinity is not really a number, so it would not be proper to call what we do substituting. Likewise, the limit algebra is not a "real" algebra. Although it is possible to do the limit algebra properly with definitions and theorems and all, most profs do not bother, which makes the limit algebra kind of illegal, some profs are even allergic to when you start treating infinity as a common number. To be on the safe side, do calculations with infinity on the side; here in our calculations we put them, along with other remarks, between big double angled braces ⟪ and ⟫ to indicate that they are not parts of the "official" solution.

One last remark concerning this substituting business. When the expression involves a general power, we should always rewrite it into the "e to ln" form.

We can rewrite both theorems in another way. They can be used to delay some parts of the limit for later, to split the limit into parts so that we can apply different methods to each part etc. The basic idea is that we can "pull things out of the limit" so that what is left in it becomes simpler. The first theorem allows us to perform algebraic operations outside of limits, assuming that what we get at the end makes sense. The second theorem allows us to pull out nice (continuous) outer functions out of limits, again assuming that what we get in the end makes sense.

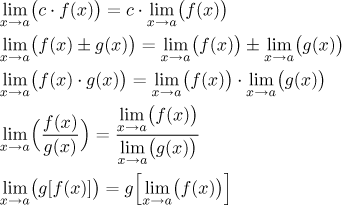
Example: We will put all details into it to show how we think. An experienced student would write just the first and the last line.

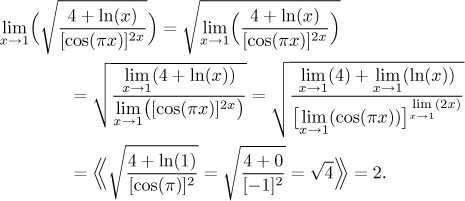
We could actually find this limit using the "substitute and see" method, but we wanted to show the use of these rules on something simple.

Note that the equalities in the rules above are "conditional". When you split a limit into several smaller ones, you do not know whether this equality is correct. Only after you finish calculating all the smaller limits, put the outcomes together using limit algebra and it makes sense, then you can say that the equality was correct and the final outcome is a valid answer to the original limit.

On the other hand, if you finish all individual limits and it turns out that you cannot put these answers together using the limit algebra, then the conditional equality is wrong, the original limit might be anything. A simple example: The constant function 1 has limit 1 at infinity. However, if we write it as 1 = (1 + x) − x and calculate the limit at infinity of each term separately, we get something that does not make sense: ∞ − ∞.

A small modification of this example shows a very important rule: Unless you know what you are doing, always finish all parts. In particular, if you split a limit of a product into a product of smaller limits and one of them comes up as zero, you cannot stop calculations and claim that the whole thing is zero. Granted, zero times a number is again zero, but that only works in the usual algebra. In the limit algebra we can also have "zero times infinity", which is an indeterminate product that can be anything. Returning to that simple example, we can try the limit at infinity like this:

lim(1) = lim((1/x)⋅x) = lim(1/x)⋅lim(x) = 0⋅∞.

Obviously it would be a mistake to stop once we saw that the first limit was zero, but after completing the other part we see the indeterminate product and know that it was not a good idea to split the original limit into two. For more details, see this note.

When using these rules and approaches, one might encounter several problems. One possible problem is that you use the limit algebra and end up with an indeterminate expression. Then one has to use various tricks to (try to) figure out the outcome. Some tricks come in the following sections, a practical review of useful methods can be found in Methods Survey.

Another problem we sometimes stumble upon concerns one-sided limits. Namely, when substituting into some functions, we can only go from one side, which should be somehow reflected in this limit algebra. For instance, we cannot write ln(0) = −∞, since the logarithm does not exist on some reduced neighborhood of 0. It only exists on a reduced right neighborhood of 0, which we wrote as ln(0⁺) = −∞. What if we have to substitute some expression leading to zero into logarithm?

Example: We will look at the limits of f (x) = ln(x²) and g(x) = ln(x³) at a = 0. If we try to use the limit algebra, in both cases we get ln(0). However, the first limit exists and is equal to −∞, while the second limit does not even make sense. Indeed, for the function f the domain is all numbers apart from 0, so limit at 0 makes sense, and as we approach 0 with x, the square makes x into even smaller positive numbers and the conclusion follows. On the other hand, the function g is only defined on (0,∞) and thus we cannot take a limit at 0.

Similarly, we often run into trouble with the expression 1/0. We know from the graph of 1/x that the limit at 0⁺ is ∞ and the limit at 0^- is −∞. This fact about one elementary function also becomes another rule in the limit algebra:

1/0⁺ = ∞     and     1/0^- = −∞.

In a simple straightforward situation with a one-sided limit we simply use the above rules, but what if we have a function that goes to zero in the denominator? For instance, 1/x² and 1/x³ behave very differently around 0. Also other functions than ln(x) and 1/x require one-sided approach (tangent, cotangent etc.) Can we find some general method that could be used to solve such cases in a simple way?

This problem is fixed by considering one-sided results to limits. We will cover this in the next part.

If we want to use the limit algebra in a situation when we compose functions and the outer function requires a one-sided argument, we can only work out the answer if we know some information about the outcome of the limit of the inside function. This suggests that we look closer at how a limit value is approached. Compare these three graphs:

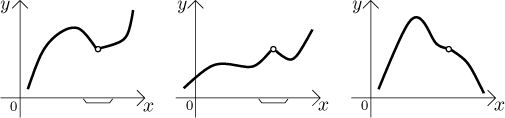
In all three cases the limit at a = 2 is equal to 1, but in different ways. In the left picture we approach this limit from above, that is, we approach it with numbers larger than 1. Larger means to the right, so we may say that we approach the limit result 1 from the right and denote it 1⁺ (we got to 1 from larger numbers, therefore "plus"). In the middle picture we approach this limit value from below, that is, we approach it with numbers smaller than 1; we denote such result 1^- (we go to 1 from smaller numbers therefore "minus"). In the last case we do not have 1⁺ nor 1^-, it is simply 1.

Definition.
Let a be a real number, ∞, or −∞. Let f be a function defined on some reduced neighborhood of a, assume that f has a proper limit L at a.
We denote this limit L⁺ if there is some reduced neighborhood of a such that f > L on that neighborhood.
We denote this limit L^- if there is some reduced neighborhood of a such that f < L on that neighborhood.

Similarly we define L⁺ and L^- for outcomes of one-sided limits.

In most cases such distinction is irrelevant, we simply say the limit is 1 and it works, but in some cases this can be very important.

We return to the example above, when we looked at limit at 0 of the functions f (x) = ln(x²) and g(x) = ln(x³). When we look at the inner functions x² and x³, we see that in both cases they have limit 0 at 0, and we run into trouble when we try to substitute this outcome into the logarithm. However, we know that ln(0⁺) does make sense, so this is a clear indication that we should look closer at the results of the limits of x² and x³ at 0.

When x approaches 0, then the function x² goes to 0 and also x² > 0. Thus the outcome of this limit is 0⁺, therefore we can put it into logarithm:

On the other hand, even when x is very close to 0, then x³ can be both positive and negative, therefore its limit at 0 cannot be written as 0⁺ or 0^-. Consequently we cannot put it into logarithm, a clear indication that there is something fishy about ln(x³) around 0.

Similarly we now easily determine the limit of 1/x² at 0, we substitute and use the limit algebra: The answer is

1/(0²) = 1/0⁺ = ∞.

However, 1/x³ cannot be done this way. What next? We usually try to look at one-sided limits, since then the extra information often gives one-sided results.

Example: Compare the following two problems:

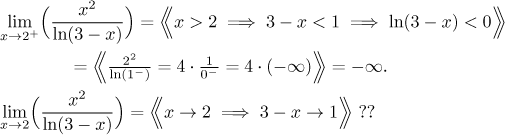
In the first problem we argue like this. When x goes to 2 from the right, it means that x is something like 2 plus a little bit, say 2.001. Then (3 − x) is 1 minus a bit (for x = 2.001 we get 0.999). When logarithm is applied to a number smaller than 1, it becomes negative. Thus we conclude that the zero, which is the outcome of the usual calculation ln(3 − 2), is actually "zero minus" and we can substitute into the fraction.

On the other hand, if x goes to 2 from both sides and gets close, then the logarithm comes up almost zero, but sometimes positive and sometimes negative, depending on which side of 2 x is. Since we are unable to specify the 0 in the denominator, we cannot make any conclusion. In fact, since we cannot force the 0 to be plus or minus, we suspect that the limit in question does not exist. To check we try to look at the limit at 2 from the left:

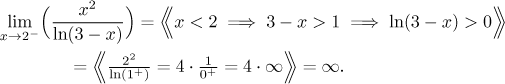
Since the limit at 2 from the right is different than the limit at 2 from the left, the conclusion is that the limit at 2 does not exist.

Remark: Although very often one-sided results appear when calculating one-sided limits, these two are not really related. One can get a one-sided result when calculating a both-sided limit, we saw such situation when looking at the limit of x² at 0. On the other hand, it can also happen that one has a one-sided limit, but the answer is not one-sided. For example, the limit of x⋅sin(1/x) as x goes to 0 from the right is 0, but thanks to the wild and never ending oscillation, the function never settles down to a positive or negative part, hence the result of this limit cannot be 0⁺ or 0^-. For more info about this function (for instance its graph) see sin(1/x) in Theory - Elementary functions.

Theorem.
If a function converges at some a, then it must be bounded on some reduced neighborhood of a.

This definitely does not go the other way around, the example of sin(1/x) in Theory - Elementary functions shows that a bounded function even need not have a limit, to say nothing about convergence. This theorem also has appropriate versions for one-sided limits and one-sided reduced neighborhoods.

Now we will look at monotonicity. The existence of a limit (or convergence) does not imply anything about monotonicity, which seems clear, we know that a function can go to its limit in crazy ways. However, we do get some information out of monotonicity.

Fact.
A function that is monotone on some reduced left neighborhood of a point a has a limit at a from the left.
A function that is monotone on some reduced right neighborhood of a point a has a limit at a from the right.

Here a may be also improper. We get more if we put together boundedness and monotonicity.

Fact.
A function that is monotone and bounded on some reduced left neighborhood of a point a has a convergent limit at a from the left.
A function that is monotone and bounded on some reduced right neighborhood of a point a has a convergent limit at a from the right.

Corollary.
A function that is monotone on an interval has convergent one-sided limits at all its inner points and also the appropriate one-sided limits at endpoints must exist.

Again, this includes the case of improper endpoints.

We start with a nice theorem.

Theorem (Heine).
Let a be a real number, ∞, or −∞. Assume that a function f has a limit L at a. Then for every sequence {a_n} such that a_n→a and a_n ≠ a we have f (a_n)→L.

We used this theorem when working with sequences. This theorem also works in the opposite direction, but it is not really good for finding limits of functions, since we would have to try all possible sequences that go to a, substitute them into f and see what they do before we could say anything about the limit of f.

However, as stated this can be useful in showing that some limit does not exist.

Example: We will show that sin(x) does not have a limit at infinity.

Consider two sequences, x_n = πn and y_n = π/2 + 2πn. They both go to infinity. What do we get when we substitute them into the sine?

sin(x_n) = 0 for every n, therefore sin(x_n)→0. On the other hand, sin(y_n) = 1 for every n, therefore sin( y_n)→1.

Now if the sine had a limit at infinity, then by the above theorem, both {sin(x_n)} and {sin( y_n)} would have to go to that limit. Since they go to different places, there is no limit of sine at infinity.

You can learn more about the interplay between functions and sequences in section Sequences and functions in Sequences - Theory - Limits.

Limit and comparison
Back to Theory - Limits