Tricks with MVT

The Mean value theorem can be used to do some interesting things.

Comparing functions

Fact.
Let f and g be functions continuous on an interval I and differentiable on its interior Int( I ). If f ′ = g′ on Int( I ), then there exists a constant C such that f (x) = g(x) + C on I.

If moreover there is a point c in I such that f (c) = g(c), then f = g on I.

We obtain this statement by considering the difference g − f and applying appropriate statements from Derivative and monotonicity. The meaning is quite clear. If two functions have the same derivative, then the tangent lines at corresponding points should have the same slopes, or to put it another way, their graphs should go up and down in the same way. When you imagine that two pencils start at a certain distance above one another on the left end and then they move to the right at the same speed and copy one another's rise and fall, you reach the obvious conclusion: One graph should be just a shift of the other, they are in a sense parallel.

If the two graphs also share a point and they are parallel, then they must be the same. This is used to prove that two expressions are equal in situations when we cannot do this using algebra.

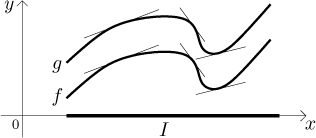
Example: Prove that for x > 0 one has

Solution: There does not seem to be some obvious algebraic approach to this equality. We therefore use the Fact above. We define f (x) = arctan(x) and g(x) = π/2 − arctan(1/x), consider the interval I = (0,∞). First we look at derivatives of the two functions:

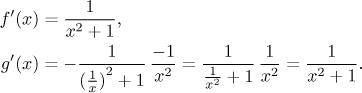
Thus the two functions are parallel. Now we need to substitute some point in to show that they are equal. We try x = 1.

By the fact above, the two functions are equal.

Note that sometimes it is not easy to find a suitable point to substitute. Then one can use a trick and compare limits, for instance at endpoints. Here we can compare like this:

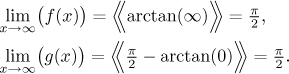
Similarly we can prove inequalities, but there we have to be a bit more careful.

Fact.
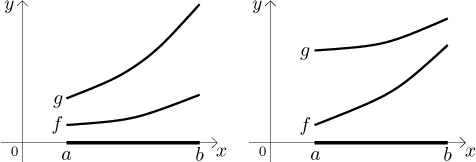
Let f and g be functions continuous on an interval I = [a,b) or I = [a,b] and differentiable on its interior (a,b). If f ′ ≤ g′ on (a,b) and f (a) ≤ g(a), then f  ≤ g on I.

Let f and g be functions continuous on an interval I = (a,b] or I = [a,b] and differentiable on its interior (a,b). If f ′ ≥ g′ on (a,b) and f (b) ≤ g(b), then f  ≤ g on I.

Here are typical situations for the two versions:

Often we use these statements with one function equal to zero, that is, to prove that, say, a given function is not negative:

Let f be a function continuous on an interval I = [a,b) or I = [a,b] and differentiable on its interior (a,b). If f ′ ≥ 0 on (a,b) and f (a) ≥ 0, then f  ≥ 0 on I.

All these comparison statements have "sharp" versions, we will show it for the last statement:

Let f be a function continuous on an interval I = [a,b) or I = [a,b] and differentiable on its interior (a,b). If f ′ ≥ 0 on (a,b) and f (a) > 0, then f > 0 on I.

Assume that we have a nice (continuous) function on an interval I. Assume that it has two zero points in this interval. Then, logically, it must have a hill or a dip between these two zero points, and if we have differentiability, then Rolle's theorem claims that there is some point between the two zero points where the derivative is zero. If we have more zero points, we can look at all successive pairs of them and for each of them find a place with derivative equal to zero.

Fact.
Let f be a function continuous on an interval I and differentiable on its interior Int( I ). If f has k distinct zero points in I, then its derivative f ′ must have at least k−1 distinct zero points in I.

If the derivative is differentiable, we can do another such step. By induction we get

Corollary.
Let f be a function with n−1 continuous derivatives on an interval I and the n-th derivative on its interior Int( I ). If f has k distinct zero points in I (where k > n), then its n-th derivative f ⁽ⁿ⁾ must have at least k-n distinct zero points in I.

This fact is sometimes used to show that some function does not have lots of zero points. We assume by contradiction that it does, then we look at its derivatives and hope for some problem.

Example: Prove that the cubic polynomial f (x) = x³ + x has at most one root.

By contradiction, assume that it has two or more roots. Take any two of them, then by the Fact above the derivative would have to have at least one zero point. However, this is not possible, since f ′(x) = 3x² + 1 > 0. Thus the assumption of two or more roots was wrong and we are done.

A direct approach is also possible, since the above Corollary can be stated equivalently as follows.

Corollary.
Let f be a function with n−1 continuous derivatives on an interval I and the n-th derivative on its interior Int( I ). If the n-th derivative f ⁽ⁿ⁾ has k distinct zero points in I, then f can have at most k+n distinct zero points in I.

Note that one has to be lucky to be able to use this trick successfully. A more reliable way to count roots is to determine monotonicity of the given function, which is usually simple once we have its derivative (see Monotonicity in Theory - Graphing), and even a symbolic sketch show clearly how many roots there are.

Back to Theory - Mean value theorem