Monotonicity and local extrema

In this section we will assume that the function that we investigate is "nice" in the sense that its domain can be split into subintervals in such a way that on each of them the function is strictly monotone and differentiable. Of course, not every function has this property, for instance the Dirichlet function (in Functions - Theory - Elementary functions) does not have a single interval in its domain on which it would be monotone. Fortunately, functions we meet almost always fall into the "nice" category.

The core of this section is identifying intervals of strict monotonicity. The main tool is the theorems from Derivative and monotonicity in Theory - MVT. From them we can deduce the following:

Fact.
Let f be a function. Assume that for some a < b < c this function is increasing on (a,b) and decreasing on (b,c), or decreasing on (a,b) and increasing on (b,c). Then either f ′(b) = 0 or f does not have a derivative at b.

This inspires the following definition.

Definition.
Let a function f be defined on some neighborhood of a point c. We say that c is a critical point if f ′(c) = 0 or f ′(c) does not exist.

Some authors also call these points stationary points. The above fact is an implication, so not every critical point separates intervals of different monotonicity, but critical points are natural candidates.

The first step in investigating monotonicity of a function f : We start with the intervals that constitute the domain of f. Then we find all critical points. These will further split the intervals of the domain into subintervals. On each of the resulting intervals the function is strictly monotone.

Since the Fact above is an implication, it may happen that we split the domain at a critical point although there is no change in monotonicity. Thus we will have to include in the next step some way to recognize "false" dividing points and join intervals when possible. From practical point of view this means that we need not worry too much about taking extra dividing points. This mainly concerns the second condition for critical points: We do not have to precisely determine at which points there is no derivative, we save time and simply take all points where the derivative looks fishy (for instance where two different formulas meet when investigating split functions).

To find out what kind of monotonicity we have on these intervals we use this theorem:

Theorem.
Let f be a function continuous on an interval I and differentiable on its interior Int(I ).
If f ′ > 0 on Int(I ), then f is increasing on I.
If f ′ < 0 on Int(I ), then f is decreasing on I.

The second step in investigating monotonicity of a function f : For each interval from the first step we find out what sign the derivative has inside this interval. Since the sign must be the same on such an interval, the easiest way to determine the signs is to pick some point from inside the interval and put it into f ′. The signs then determine monotonicity. For an example look below.

Question: Not every critical point really separates intervals of different monotonicity. What happens when we use in the above procedure such a "false" dividing point?
Answer: Nothing that could not be fixed, we simply split an interval that should be just one into two. In other words, after we finish with step two, we should scan the situation for adjacent intervals of the same monotonicity and ask whether they can be connected. Sometimes this is simple, we can always connect adjacent intervals of identical monotonicity if the function is continuous at the point where they meet. Otherwise we have to check on what is happening at the dividing point, for details see Monotonicity in Functions - Theory - Real functions.

Question: When do we put open and when closed intervals in the answer?
Answer: We always try to show maximal intervals of monotonicity. That's why we should try to connect intervals if possible (see the previous question) and that's why we should try to include endpoints of intervals if possible. However, here people tend not to be too dogmatic about it. The easy case is when the function is continuous at a given endpoint from the appropriate side (for a right endpoint we need continuity from the left and vice versa), then we can include it. If we do not have continuity, we would have to do more work, but traditionally we do not bother and simply leave such endpoint open. It is actually quite convenient that closed endpoints of intervals of monotonicity indicate continuity.

Here we again have a statement that allows us to look only at a small set of candidates.

Theorem.
Let a function f be defined on some neighborhood of a point c. If f has a local extreme at c, then c must be a critical point.

So to find local extrema we first find all critical points and then investigate them. For classifying extrema we have a theorem in Derivative and monotonicity in Theory - MVT, but it is rarely used. First, it is not reliable, and second, we usually look for local extrema in situations where we also investigate monotonicity, and we can easily classify local extrema using the information on monotonicity.

Fact.
Let f be continuous at c.
If there is a right neighborhood of c on which f is increasing and a left neighborhood of a on which f is decreasing, then f has a local minimum at c.
If there is a right neighborhood of c on which f is decreasing and a left neighborhood of a on which f is increasing, then f has a local maximum at c.

If we do not have continuity, we have to investigate closer using one-sided limits and knowledge of monotonicity around c. There are many cases and it is not worth going through all of them, common sense should suffice. For instance, consider the following cases:

In the first, third and fifth picture we have a local maximum at c, while the second and fourth picture shows functions that do not have a local maximum at c.

We refer to Monotonicity in Methods Survey - Graphing for practical overview.

Example: Investigate monotonicity and local extrema of f (x) = x⁴ − 4x³.

Solution: The domain is the whole real line, so there is one starting interval, namely (−∞,∞).
We find the derivative: f ′(x) = 4x³ − 12x² = 4x²(x − 3).
Critical points: f ′(x) = 0 yields x = 0 and x = 3; there are no points where f ′ does not exist.
Thus we have three intervals of monotonicity: (−∞,0], [0,3], and [3,∞), we used closed intervals where f is continuous.

We substitute x = −1 into f ′ to see that f ′ < 0 on (−∞,0]. Substituting, say, x = 1 into f ′ we see that f ′ < 0 also on [0,3]. Finally, we try x = 4 to find out that f ′ > 0 on [3,∞).

We see that f is decreasing on the first two intervals and increasing on the third one. We have the same monotonicity on adjacent intervals, can they be connected? Since f is continuous at 0, the answer is positive. Thus the conclusion is that f is decreasing on (−∞,3] and increasing on [3,∞).

Critical points are also candidates for local extrema. By looking at the monotonicity pattern we conclude that there is no local extreme at 0 and that f (3) = −27 is a local minimum. By the way, the function looks like this:

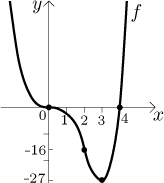
This procedure can be streamlined using a table. For details see Monotonicity in Methods Survey - Graphing.

Concavity
Back to Theory - Graphing functions