Taylorův polynom a aproximace: Přehled metod

Problém: Najděte Taylorův polynom stupně n se středem a pro danou funkci f.

Případ 1. n je konkrétní číslo.

Algoritmus:
Krok 1. Najdeme derivace f až po řád n.
Krok 2. Dosadíme a do všech těchto derivací.
Krok 3. Použijeme vzniklá čísla k vytvoření polynomu

Pro další informace viz Taylorův polynom v části Teorie - Aplikace.

Příklad: Najděte Taylorův polynom čtvrtého stupně se středem a = 1 pro f (x) = e^2x.

Řešení: Najdeme potřebné derivace a dosadíme do nich a.

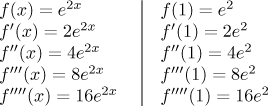
Teď sestavíme žádaný polynom.

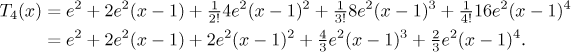
Případ 2. n je obecné.

Algoritmus:
Krok 1. Najdeme derivace f až po dostatečně vysoký stupeň, obvykle stačí 4 nebo 5.
Krok 2. Do všech těchto derivací dosadíme a.
Krok 3. Tipneme, jak vypadá k-tá derivace pro obecné k. Stačí uhádnout f ^(k)(a), takže je možné hádat po Kroku 2, ale často je snažší hádat obecně f ^(k)(x), protože pak je lépe vidět, jak se ta derivace vytváří, a teprve po uhodnutí dosadíme daný střed a.
Krok 4. Použijeme těchto čísel k sestavení polynomu

Vyjádřit jej pomocí sumy bývá dobrý nápad.

Příklad: Najděte Taylorův polynom stupně n se středem a = 1 pro f (x) = e^2x.

Řešení: Už jsme našli první čtyři derivace.

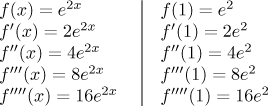
V levém sloupci vidíme, že při každé derivaci "přidáme" další 2 do násobení, přidáme jich tolik, kolik je řád derivace. Odhadneme proto, že f ^(k)(x) = 2^ke^2x, což se dá dokázat indukcí, po dosazení středu dostaneme f ^(k)(2) = 2^ke². Ověříme, že se to shoduje s prvními čtyřmi derivacemi, které už jsme předtím měli. Můžeme tedy napsat výsledek.

Aproximace

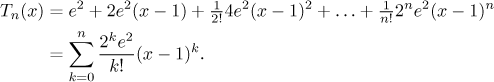
Problém: Aproximujte f v určitém bodě b pomocí Taylorova polynomu daného stupně.

Algoritmus:
Krok 1. Vybereme vhodný střed a. Dva požadavky: Měl by být co nejbližší k b a neměli bychom mít moc problémů při dosazování a do f a jejích derivací.
Krok 2. Najdeme Taylorův polynom daného stupně se středem a z Kroku 1 (viz výše).
Krok 3. Odhadneme f (b) číslem T(b).

Příklad: Aproximujte ln(1.2) pomocí Taylorova polynomu stupně 2.

Řešení: Která čísla se snadno dosazují do f (x) = ln(x)? Například 1, e, e² atd. Nejblíže k 1.2 je a = 1. Použijeme proto T₂ s tímto středem. Začneme spočítáním nutných derivací.

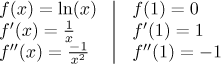
Sestavíme polynom:

Teď můžeme aproximovat.

Mimochodem, jak dobrý je tento odhad? K odhadu chyby použijeme Lagrangeův tvar zbytku.

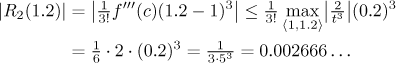
Teď víme jistě, že ln(1.2) = 0.180±0,003.

Pro další příklady viz Taylorův polynom v části Teorie - Aplikace a Řešené příklady - Aplikace, zajímavé použití lze najít v tomto příkladě v části Řady - Řešené příklady - Testování konvergence.

Zajímavý speciální případ je Taylorův polynom stupně 1, tedy tečna. Pro jednu užitečnou aplikaci viz Aproximace v části Teorie - Aplikace.

Zpět na Přehled metod - Aplikace