Example: Evaluate the integral
![]()
Solution: The "extra cosine" next to dx just calls for the sine substitution.
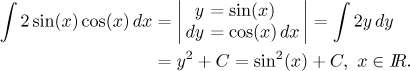
We also have an "extra sine", so check for yourself that the
substitution
![]()
Some reader surely thought that the expression in the integral feels familiar. That is the third possible solution, first simplify the integral using a trig identity and then use substitution.
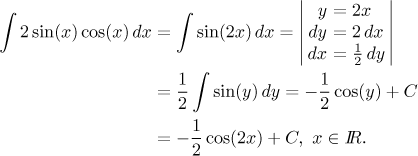
It seems that we obtained three different answers, since clearly none of the following equations is true:
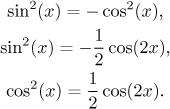
The secret here lies in the magical constant +C representing an
arbitrary number. It does not have to be the same number in those three
results, so in fact we should have used different letters there - and this is
where the difference is hiding. Indeed, those three algebraic expressions
above are not the same, but they differ only by a constant and therefore are
all antiderivatives of
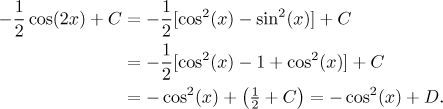
The moral of the story is that if it happens that your calculations lead to a different result than somebody else's, it does not mean that one of those results is wrong - they may simply differ by a constant. When in doubt, check by differentiating.
When looking for solutions we were guided by intuition. If we tried the approach through boxes, then we would have to ask the box trigonometric integrals a the advice would lead to the three solutions above.
This integral can be also solved in two more ways, namely using integration by parts. Does it fit this type? It is a product and we can easily integrate one part. The second part is supposed to improve by differentiation, that does not work here, so tis is not exactly the best by parts candidate. Nevertheless we will try it and see what happens.
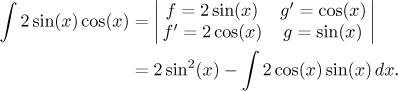
Surprisingly we ended up with the same integral, which is not really a problem, we move it to the other side and obtain an equation. Here it is important to note that antiderivatives on the right can differ from those on the left by a constant, so after subtraction there will be that constant left on the right.
![]()
I'll be, that's exactly the first result. By the way, was there any reason
for taking the sine for f? Actually, no there wasn't, we just took it
from the left. One can as well take the cosine for f and the sine for
We see that this problem can be solved in at least five different ways. It is a pity that we do not get two more different results from integration by parts and I regret that one cannot solve this integral using partial fractions, then we would have shown all basic methods here. But it is a nice problem all the same.