Integration "by parts" is based on an identity that can be expressed for instance like this:
![]()
(See integration by parts in Theory - Methods of Integration for other possibilities and further information.) The main idea of this method goes as follows: You are given an integral and you succeed making it fit the integral on the left in the above identity. Then you can pass to the expression on the right. Of course, this makes sense to do only if the new integral on the right is easier (or the same, see below).
Algorithm for integration by parts.
Step 1. Express the integrated function as a product of two
expressions; denote one of them
Step 2. Determine the other two expressions that appear in the formula.
Namely,
Step 3. Plug those expression into the by parts formula. This
concludes the procedure and now you can attempt to evaluate the new integral
on the right hand-side.
It is traditional to mark the use of integration by parts into a matrix, we put f and g′ into the first row and calculate f ′ and g in the second row. We will show an example now.
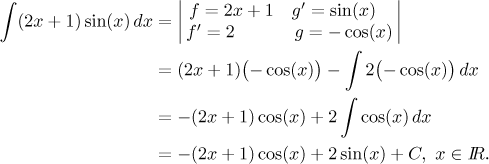
Note that the whole expression in the given integral must be included in the procedure, so when we multiply the two expressions in the first row of the matrix, we must get exactly the expression in the integral. It is not possible to set a part of the given integral aside. As we can see, in the second row of the matrix we find the new integral.
Experienced integrators sometimes do not write this matrix, integration by parts goes like this: First you integrate a part of the given expression and thus you get the irst new term, the one that is already done. In this new term you then differentiate the other half and you get the new integral.
There are two things to consider. First, the part that we intend to
integrate, that is, the one that we chose for
Secondly, the rest, that is, the part that we intend to differentiate and
denote by f, should get markedly better when differentiated (It is
exactly here where we should make sure that the new integral will be
simpler). Again, when we imagine erivatives of various expressions, we
realize that also here we do not have much choice.
When we put it together, we end up with essentially three types of integrals where it makes sense to apply integration by parts. It is a good idea to remember them.
• The type "removing x".
We saw an integral of this type at the beginning of this section, in product
we have a function that can be integrated easily multiplied by a
polynomial that we reduce using differentiation. Basic examples:
![]()
We take the power of x (or more generally a polynomial) as f
and that easily integrable function as
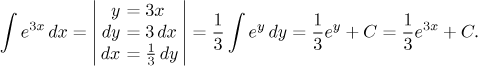
Now we can evaluate the following integral, an obvious candidate for removing x using integration by parts.
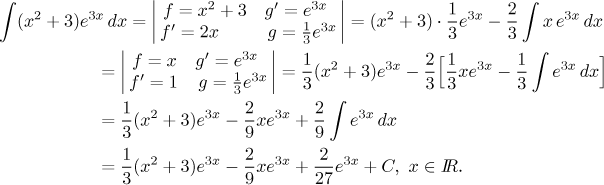
One of the most frequent integration mistakes is to forget the brackets when repeating integration by parts. Note that this method would not help if the power of x did not have exponent equal to a positive integer. Convince yourself that you cannot get rid of, for instance, a square root of x by differentiation.
• The type "removing logarithms".
This approach is based on the observation that by differentiating a
logarithm we get a power, so the new integral would be without any logarithm
at all. We use this approach for integrals like
![]()
Here we do it the other way around, we take the power of logarithm as f
and the power of x (or a polynomial) as
Of special interest is the last integral. You probably already noticed that
logarithm is suspiciously missing in the table of elementary integrals. The
reason is obvious, logarithm is not a derivative of any elementary function
and its integral is usually evaluated (unless we remember it or find it
somewhere) using integration by parts and a curious (and tricky) choice
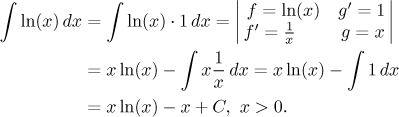
• The type "removing inverse trigonometric functions".
Inverse trigonometric functions are similar to logarithm in that their
derivatives are of a completely different kind and much better from the
point of view of integration. Thus one can apply similaer trick to integrals
like these:
![]()
As an example we will show the important integral of arc tangent, where we again use the trick with 1.
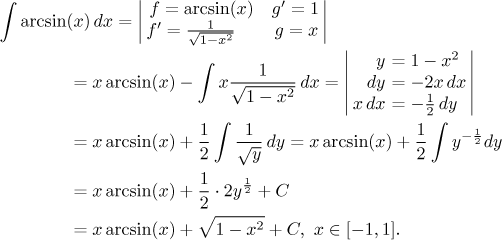
The reader will meet integration by parts most often in connection with the three types listed above, but this method can be used also in other situations, sometimes in a surprising way. We will now show one quite a useful trick.
Trick with an equation:
We use this trick for problems where, after (several) "by
parts"
calculation(s), we get the same integral we started with, just with the
opposite sign. This is best explained by an example:
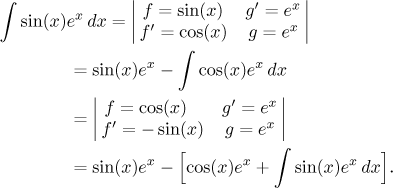
We get an equation
![]()
If we move the integral on the right hand-side to the left hand-side (keeping in mind that these are two sets of antiderivatives, so they may differ by a constant and this constant stays on the right), we get
![]()
and hence
![]()
(We denoted C=D/2. If D is some (arbitrary) constant, then the same is true for D/2, so we can denote it by some letter.)
This particular type of integral is also quite useful in some applications and the result we just obtained can be found in more extensive lists of integrals. Two more situations with equations can be found in this problem and this problem in Solved Problems - Integrals.
Remark: Note that the antiderivative we take for g need not be the simplest one, with C taken as 0. Sometimes it may be to our advantage to use a different value in order to help us with the new integral. Consider the following problem. It is a typical speciment of the type "removing logarithm" and we apply integration by parts in the usual way.
![]()
To finish the problem we would have to first divide the polynomial and then integrate the remainder, which is not difficult, but why work if we do not have to. A simple trick rids us of that fraction.
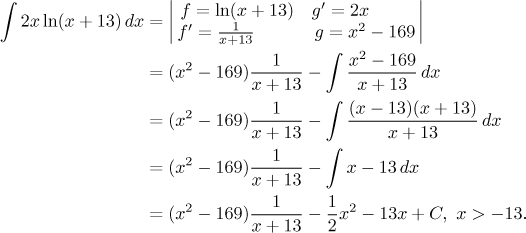
Much better. This does not happen often enough to spend much time on it, but it is good to be aware of the fact that there is in fact some freedom in choosing g.
Integration by parts is also behind some useful formulas, see this note and this note. As we also saw, integration by parts yields integrals of several basic functions, so it is quite an important method. Typical use of it can be found in this problem, this problem and this problem In Solved Problems - Integrals.
Next box: rational functions
Back to Methods Survey
- Methods of integration