Volume of a solid of revolution

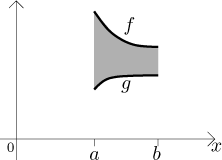
Consider the region R bounded from above by the graph of a function f and from below by the graph of a function g on an interval [a,b].

Disc method:

Consider the solid obtained by rotating the region R about a horizontal axis of rotation given by y = A, where A < min(g).

Its volume is equal to

Shell method:

Consider the solid obtained by rotating the region R about a vertical axis of rotation given by x = A, where A < a.

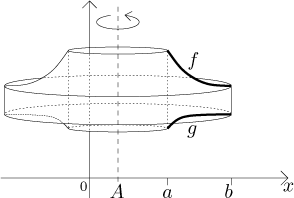
Its volume is equal to

More complicated regions have to be decomposed into regions of the above type.

Example: Consider the region under the graph of f (x) = 1/x on the interval [1,2]. Find the volume of the solid obtained by revolving this region abound the axis given by y = −3.

Solution: We start with a picture:

We see that in fact we have a region bounded from above by the function f (x) = 1/x and from below by g(x) = 0. Since we rotate around a horizontal axis, we should use the disc method:

If the integral is too difficult, sometimes it helps to switch the axes (see Area). Actually, our example above was easy, but we will use it to show the axes switching anyway. We turn the picture around the diagonal, changing to inverse function for the graph:

We see that we have to divide the rotated region into two parts. First, we rotate a rectangle between functions x = 2 and x = 1 on the interval [0,1/2], then we rotate the region between functions x = 1/y and x = 1 on the interval [1/2,1]. Since we flipped the axes, we have to integrate with dy; vertical axis of rotation means that we should use the shell method:

Adding these two volumes together we get the total:

This way it was more difficult. After gaining some experience, it is usually easy to see from the shape of the region whether it pays off to switch the axes.

Just like with the area, there are two possible approaches to finding the volume. One is to remember the above pictures and formulas and apply them, which may get a bit confusing in more complicated situations. The other approach is to remember the idea behind the disc and shell methods, that is, the trick with thin revolving stripes, and apply it to a given problem. This approach, when mastered, may be easier especially in the situation when we would like to switch axes. We show it in this solved problem.

Volume of a solid of rotation given by a parametric curve

Consider a parametric curve x = x(t), y = y(t) for t from [α,β]. Assume that y(t) ≥ 0 for all t and that x(t) is monotone. Consider the region under this curve.

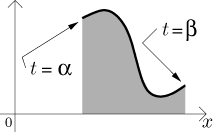
The volume of the solid obtained by revolving this region about a horizontal axis of rotation given by y = A, where A ≤ 0, is

The volume of the solid obtained by revolving this region about a vertical axis of rotation given by x = A, where A < min(x(t)), is

Surface of a solid of revolution
Back to Methods Survey - Applications