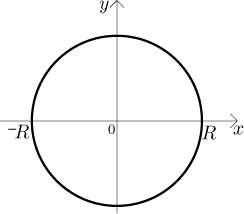
Problem: Find the area of a disc of radius R.
Solution: We position the disc with its center in the origin:

First we will try it using the graph of a function approach. Since the
picture is symmetric, the area of the disc is equal to the double of the area
of the upper half. What function has its graph equal to an upper semi-circle?
Since the circle is given by
![]()
Thus the area of the circle is
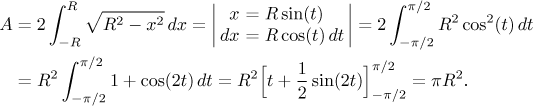
Note that the integral was a standard type from the "root of quadratics" box.
The centered circle of radius R can be also described by parametric
equations
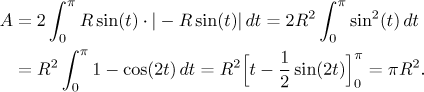
Finally, we can try do pass to polar coordinates. The centered circle of
radius R is given by the equation
![]()
Since circle is an object invariant with respect to rotation about the origin, it is not surprising that the polar coordinates lead to the easiest solution.