Here we will look at integrals of functions involving roots (but also other powers) of quadratic polynomials. There are essentially three approaches how to deal with such a situation, namely using trigonometric functions, hyperbolic functions and Euler substitutions.
There are standard substitutions that change such integrals into integrals
with trig functions. They are based on the identity
• Type integrals with
![]() .
.
Use the indirect substitution

As you can see, the root is eliminated in this way. With a bit of luck you can solve the resulting integral, then comes the back substitution (which may be a problem, see below).
An attentive reader may now argue that the substitution outlined above was
not correct. The cosine in the second line should have been in absolute
value. In this particular case it is actually correct as written. We consider
![]() (or perhaps on the interval
(or perhaps on the interval
![]() , for
instance if the root appears in the denominator), for explanation see
Indirect substitution in section
Substitution in Theory - Methods
of integration. you find some explanation why. On both of those intervals we
consider the function
, for
instance if the root appears in the denominator), for explanation see
Indirect substitution in section
Substitution in Theory - Methods
of integration. you find some explanation why. On both of those intervals we
consider the function
Example:
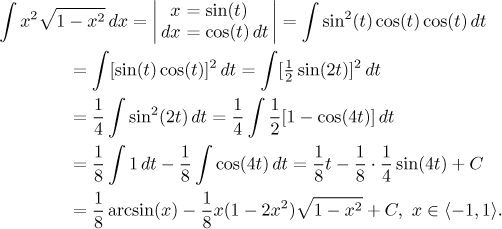
How do we make the last step? It is hard. Back substitution tends to be something of an adventure with these types of substitution and the general strategy is to rewrite the answer into a form that of all trig functions uses only the one that we have in the substitution, in this case sine. Details of this calculation can be found here.
In the following examples we will also try to write the results in such a way that they only feature functions appearing in the substitution formulas. One can also get some help from pictures of triangles, as we explain at the end of this part about trig substitutions.
• Type integrals with
![]() .
.
Use the indirect substitution
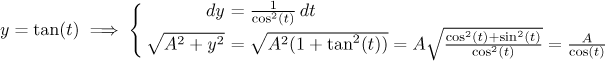
Also with this substitution we also do not have to worry about the absolute
value when handling the root. The reason for this is as before: We take
t from the interval ![]() (or somewhat smaller, see the explanation above) and
cosine is not negative there.
(or somewhat smaller, see the explanation above) and
cosine is not negative there.
The rest is similar to the previous substitution. We will show it on an example, where we also use the trick with completing the square.
Example:
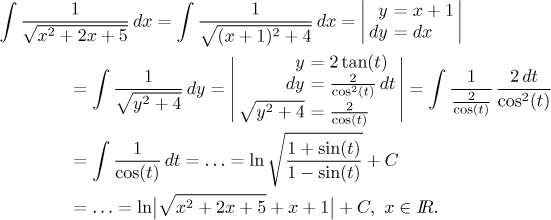
We skipped the middle part of this calculation, since here we focus on
getting rid of the root, in fact we have already shown how to integrate the
reciprocal cosine in the section on
trigonometric integrals.
Of special interest is then the last step, when we do the back substitution,
and there it is a nice piece of black magic, since we need to create
tangents in the result, also the expression
Since the back substitution was quite difficult here, it is time to talk
about alternatives. The simplest way is based on triangles We rewrite the
substitution like this:
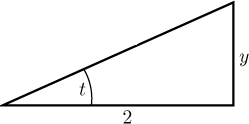
Now we just fill in the third side and find formulas for other trigonometric functions.
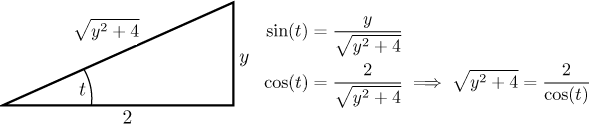
With these formulas it is much easier to do the back substitution. Note that this triangle can also help with substitution itself, since it yields the right expression for the root that we were trying to get rid of.
There is another very useful simplification. An experienced integrator would combine the two substitutions into one in this way:
![]()
We will be doing this from now on.
• Type integrals with
![]() .
.
Use the indirect substitution
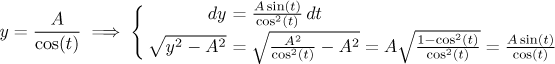
Unfortunately, here it is not so easy with the absolute value. Properly we
should actualy calculate this integrals twice, once for
But in most cases both calculations lead to the same formulas, so it is a good idea to first evaluate the integral with positive y and then check by differentiation whether this result also works also for the second interval for y.
Example:
![]()
We are supposed to use the substitution
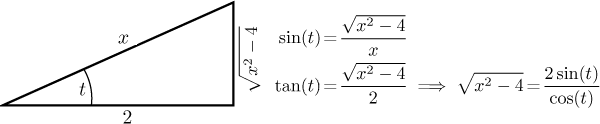
Now we are ready.
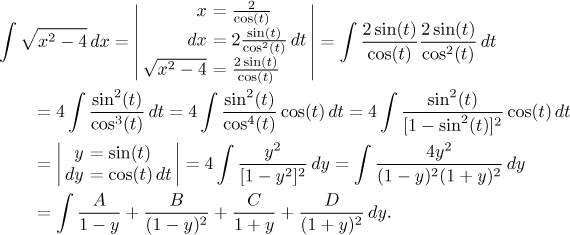
We face the
partial fractions decomposition.
Use your favorite method to
determine constants. Here we recommend the "cover-up" method to obtain
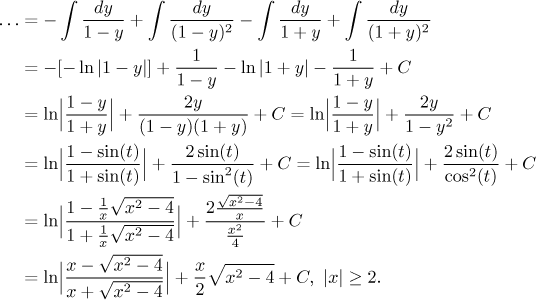
Since we did not use absolute value, the calculation is actually formally correct only for x greater or equal to 2, but when we check the answer, we find out that it also works for those negative x, so the answer is actually fine. We got lucky.
If you want to see an example where leaving out absolute value fails, try "intermediate" problem 4. in Exercises - Integration.
These offer an interesting alternative based on the identity
• Type integrals with
![]() can be
solved using the substitution
can be
solved using the substitution
![]()
As usual in this chapter, the cheating regarding the absolute value works
again, here is is obvious as
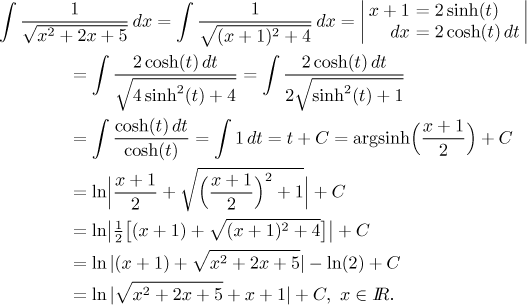
This looks somewhat easier than our original solution, but we got lucky with the easy back substitution and copied the logarithmic expression for argsinh.
• Type integrals with
![]() can be solved using the substitution
can be solved using the substitution
![]()
Unfortunately, here we cannot ignore the absolute value. We will use the approach "hope and you will be rewarded", namely we ignore absolute values and hope that the result will be correct. Only if the check by differentiation does not work out we would have to integrate twice. Now we will apply this method to the problem we solved earlier when covering this type.
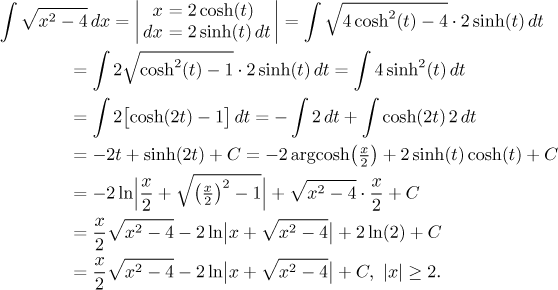
Again, the beginning of this new solution looks easier, but the back substitution is quite tough.
These represent an entirely different approach to evaluating integrals with
roots of quadratics. This method does not require any modifications of the
quadratic expression, we keep it as it is. Depending on the type of the
quadratic polynomial, we use one of the three so-called Euler substitutions.
So assume that we have an integral featuring a root (or some other power)
of an expression
• If
![]()
• If
![]()
• If the polynomial has real roots u, v, we can use the Third Euler substitution
![]()
Obviously, these situations are not mutually exclusive, so sometimes one can choose from more options. Note that the original variable always appears on both sides of those equalities, so one has to first rearrange these substitutions to be able to use them.
We will try these out on the last example above. There we can use the first and the third Euler substitution. We start with the first one and as the first step we prepare formulas.
![]()
Hence
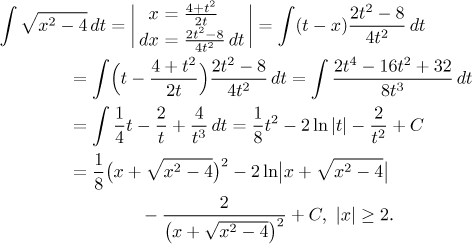
This answer is equal to the one we obtained before, as you can see when you multiply out.
Since we can factor the polynomial and one root is 2, we can also use the 3. Euler substitution:
![]()
and the integral is again transformed into a partial fractions problem. Similarly we could use the root −2.
We conclude this note with one more remark concerning one peculiarity related to the last substitution that we tried. It also shows an interesting connection of this problem with another "box".
As you can see, we have many methods for dealing with integrals with roots of quadratics. Basically, all you need to know is the three trig substitutions and you cover all cases, or all three Euler substitutions. In Solved Problems - Integrals we use these methods here and here, somewhat surprisingly also in here.