Příklad: Vyšetřete konvergenci následující posloupnosti funkcí:

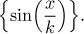
Řešení: Nejprve se podíváme na bodovou konvergenci. Budeme považovat x za parametr a spočítáme limitu vzhledem ke k. Pak jde argument sinu k 0, a protože je sinus spojitá funkce, dostaneme

Závěr: Daná posloupnost konverguje k funkci f (x) = 0 na celé reálné ose (což je tedy obor konvergence této posloupnosti).

Jak je to se stejnoměrnou konvergencí? Začneme zkoumáním rozdílu mezi f a jednou konkrétní f_k na právě zjištěném oboru konvergence.

Právě jsme dokázali, že stejnoměrná convergence nefunguje na celé reálné ose, protože suprema nejdou k nule.

Je nějaký způsob, jak se těmto potížím vyhnout? Ano. Víme, že |sin(y)| je někdy malý a někdy velký, a v počátku začíná na úrovni 0. Nejbližší číslo k počátku, ve kterém je tato funkce rovna 1, je y = π/2. Pokud se budeme držet výrazně blíž k počátku, než je toto číslo, pak se sinus nestane velkým. V naší situaci je nejbližší bod k počátku, ve kterém je sin(x/k) rovno 1, číslo x = (kπ)/2. Všimněte si, když zvětšujeme k, tak se tyto body posouvají pryč od počátku. Pokud tedy uvažujeme nějaký konkrétní interval okolo počátku, tak dříve nebo později tyto kritické body opustí náš interval a sinus tam začne být malý.

Dá se to také vidět z obrázku. Připomeňme, že funkce f_k jsou všechny jen siny se změněným měřítkem proměnné, které ty siny roztahuje od počátku.

Opravdu tedy vidíme, že každá z těchto funkcí je někde příliš velká a proto neaproximuje dobře f(x) = 0, ale ty kopce se posouvají stále dál a dál od počátku. Odhadneme tedy, že ty správné množiny pro stejnoměrnou konvergenci jsou množiny typu M = ⟨-a,a⟩ pro a > 0. Chceme pro takovou množinu najít hodnotu M_k. Všimněte si, že jakmile je a pevně zvoleno, pak pro všechna k splňující k > a jsou funkce f_k rostoucí na M a také jsou tam symetrické, takže dostaneme

Náš odhad je potvrzen, suprema jdou k nule.

Závěr: Daná posloupnost konverguje k funkci 0 stejnoměrně na množinách typu M = ⟨-a,a⟩ pro a > 0.

Další příklad
Zpět na Řešené příklady - Řady funkcí