Basic properties

Below we look at boundedness and monotonicity, the basic two properties of sequences. We will introduce the necessary definitions, explain them and show a few examples. Many simple examples can be found in the next section: Important examples, and two solved examples can be found in Solved Problems.

Boundedness

A sequence is bounded if we can restrict the size of all its terms.

Definition.
We say that a sequence {a_n} is bounded from below if there is a number k (lower bound) such that for all n we have a_n ≥ k.
We say that a sequence {a_n} is bounded from above if there is a number K (upper bound) such that for all n we have a_n ≤ K.
We say that a sequence {a_n} is bounded if it is both bounded from below and from above.

So a sequence {a_n} is bounded if there are numbers k and K such that for all n we have k ≤ a_n ≤ K.

Note that the words "for all n" mean "for all n that are used for indexing the sequence"; typically it would be for all n = 1,2,3,..., but we know that the indexing can be started at some other number than 1.

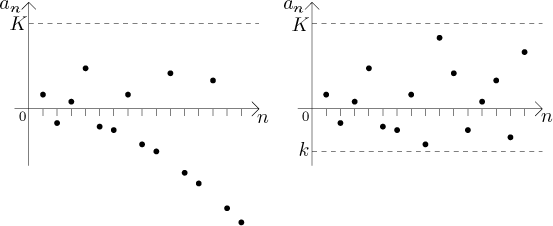
When we look at a graph of a sequence, boundedness from below means that we can draw a horizontal line so that all points representing the sequence stay above this line. Similarly, boundedness from above is true if all points of the sequence are below a certain line; boundedness means that the sequence can be "closed" between two horizontal lines.
In the picture below, the left sequence is bounded from above, but not bounded from below and therefore also not bounded. Actually, in the picture we could put a horizontal line below all the dots, but we remember that the picture shows only the beginning of the sequence, it is supposed to extend to the right to infinity preserving the suggested tendencies, and there seem to be dots going down at a regular rate; therefore, no matter where we put a horizontal line, the dots will sooner or later drop below it.
The sequence on the right is bounded, bounded from above and bounded from below.

Example: Consider the sequence a_n = (4 − 3n)/n², n = 1,2,3,...
We look at the first several terms; the sequence begins {1, −1/2, −5/9, −1/2, −11/25, −7/18, −17/49, −5/16, −23/81, −13/50,...}.

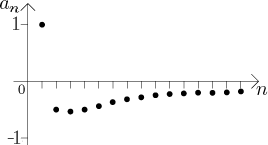
From the picture it would seem that a_n ≤ 1 and a_n ≥ − 1. If we can prove it, the sequence will be confirmed to be bounded. For the proof we will use the easiest way. We do it "from definition": We write what we want to be true and explore it to see whether it really works.

In the last line, the left inequality is true for all n ≥ 1 and the right inequality is true for all numbers n. So we ended up with true statements. Since the operations involved when going down were equivalent, we can reverse the process, so the original statements about boundedness were also true.

Note:
Clearly once we have some upper or lower bound, we can also find many others. In our example we used bounds −1 and 1, but we could have used for instance −3/4 and 13. It is usually easier to try nice numbers, proving that for all n we have a_n ≥ −3/4 is a bit more messy.

If we suspect that a given sequence is bounded, we may save some time by investigating its absolute value. For instance, in the above example we could have proved that |a_n| ≤ 1 for all n, which would do the boundedness from below and above in one step. In this particular example it does not seem any easier; however, in many examples this trick with absolute value can help.

This is in fact a general statement.

Fact.
A sequence {a_n} is bounded exactly if there is a number h so that |a_n| ≤ h for all n.

Proof: If this sequence satisfies the given condition, then obviously -h ≤ a_n ≤ h for all n, therefore the sequence is bounded.
On the other hand, if we have a bounded sequence, then we have an upper bound and a lower bound from the definition of boundedness, that is, there are k and K so that k ≤ a_n ≤ K for all n. Set h = max(|k|,|K|). Then -h ≤ k and K ≤ h, therefore -h ≤ a_n ≤ h for all n. This is exactly the condition from the Fact.

Note that boundedness is decided at "the end" of the sequence. A finite set of numbers always has its maximum and minimum, so the boundedness can be possibly violated only if we take into consideration an infinite number of terms. To put it another way, disregarding a finite number of terms of a sequence (its beginning for instance) does not change its boundedness properties. Therefore, when we investigate boundedness, we do not really care where did the indexing start; if it helps, we can disregard several first terms and only consider n > N for some fixed and suitable N.

The following two statements should seem natural: If a sequence is bounded, then all its subsequences are bounded. If a sequence has an unbounded subsequence, then the sequence itself is also unbounded.

Here we define what it means that a sequence is monotone. This is a general notion encompassing the notions increasing and decreasing.

Definition.
We say that a sequence {a_n} is increasing if for all n we have a_n < a_n+1.
We say that a sequence {a_n} is non-decreasing if for all n we have a_n ≤ a_n+1.
We say that a sequence {a_n} is decreasing if for all n we have a_n > a_n+1.
We say that a sequence {a_n} is non-increasing if for all n we have a_n ≥ a_n+1.
We say that a sequence {a_n} is monotone if it is any of the above.

For proper understanding of the definitions we have to realize the following. Given n, then a_n represents a certain term of the given sequence and a_n+1 is the term with index increased by one, that is, it is exactly the next term in the sequence. So increasing means that when we look at some term of the sequence, the next one must be larger, and this must be true for all such successive couples. Since the definition of increasing requires that the given property holds for all couples, it follows that the existence of just one couple of successive terms failing the given inequality is enough to make this sequence not increasing. Similar observations are true for the other notions in the definition.
Thus in the increasing sequence, each successive term must be larger than the previous one, throughout the sequence; a non-decreasing sequence is required to also keep going up, but it can also sometimes (or always) stay the same - the only thing forbidden is to go down somewhere. This should all become clear once you look at the four typical examples below. They are in the same order as the notions in the above definitions.

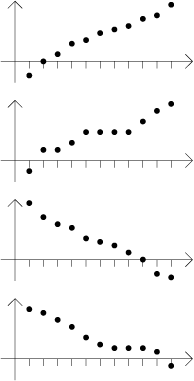
Note that there are various relationships between these notions. An increasing sequence is automatically non-decreasing, while a decreasing sequence is automatically non-increasing. There are even sequences that are both non-increasing and non-decreasing - namely all constant sequences. On the other hand, an increasing sequence can not be decreasing and vice versa.

Example: Consider the above example a_n = (4 − 3n)/n², n = 1,2,3,..., which as we saw starts like this:
{1, −1/2, −5/9, −1/2, −11/25, −7/18, −17/49, −5/16, −23/81, −13/50,...}.

What can we say about monotonicity of this sequence?
Since the second term is smaller than the first one, a₁ = 1 > −1/2 = a₂, it follows that the sequence cannot be increasing or non-decreasing (it did decrease when going from a₁ to a₂, see the discussion above). Could it be decreasing or non-increasing? No, it cannot, because it increases at one place at least, we have a₃ = −5/9 < −1/2 = a₄. The conclusion is that this sequence is not monotone.

Note that if we disregard the first two terms and consider the sequence a_n = (4 − 3n)/n², n = 3,4,5,..., which starts {−5/9, −1/2, −11/25, −7/18, −17/49, −5/16, −23/81, −13/50,...}, we get an increasing sequence. It seems to work in the picture, but a picture is never sufficient as a proof - especially since we see only a little piece of our sequence. We will cover advanced ways to prove monotonicity later (cf. Sequences and functions in Theory - Limit and Methods Survey - Basic properties), here we will do it by the definition. We start from the inequality we hope to be true and investigate it.

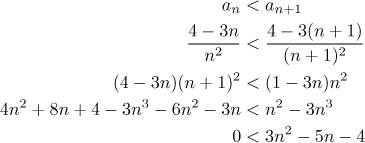
The last inequality is true for all n = 3,4,5,... (it is also true for all n < −1, but we do not care). Since we used equivalent operations, also the first inequality is true, which means that the truncated sequence is increasing, therefore also monotone.
Note how we substituted for a_n+1. This is a frequent source of trouble with beginners, but once you see how it works, it should be easy. We have a_n = (4 − 3n)/n². How do you calculate a₁₃? You put 13 instead of all n's in the formula. How do you then calculate a_k? In the same way, you put k instead of all n's in the formula. And now you just think of this with k = n + 1.

We see that unlike the boundedness, monotonicity can be changed by adding/removing some terms to/from a sequence.

However, in one direction we have a positive statement: If a sequence is monotone, then all its subsequences are monotone. A few pictures should convince you that this statement might be true. Note that also the "direction" is preserved, a subsequence of a sequence going "up" will still go "up". However, sometimes the exact type changes.

Example: Consider the sequence defined for n = 0,1,2,... as follows:

Than is, if n is even, then a_n = n/2, and if n is odd, then a_n = (n − 1)/2. The sequence goes {0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 5,...}. So this sequence is monotone, namely non-decreasing. If we form a subsequence by taking every second term, we get the sequence {0, 1, 2, 3, 4, 5,...}. As the statement said, this sequence is also monotone, and it also goes up. However, now the "quality" improved: This sequence is not just non-decreasing, but even increasing.

If we start with a sequence that is not monotone and take a subsequence, then the situation can stay the same, or it can also improve. For instance, if we take every second term from the alternating sequence {1, −1, 1, −1, 1,...} which is not monotone (see the next section, Important examples), we obtain the monotone sequence {−1, −1, −1, −1,...}.

Monotonicity sometimes helps when exploring convergence, see Basic properties in Theory - Limit.

Important note.
Unfortunately, the terminology above is not generally accepted. It is favored by many authors, but many authors also favor a competing terminology. Instead of the notions (in the above order)
increasing, non-decreasing, decreasing, non-increasing
they use
strictly increasing, increasing, strictly decreasing, decreasing.
They use monotonicity as above, but for the first and third notion they also use the common name strict monotonicity.

This confusion is unfortunate, but fortunately it does not lead into a big trouble. In theorems we usually require that a sequence is monotone, at the definition of which both schools agree. All in all, as usual, the prof giving the course you are attending is always right, so check which terminology he/she uses and stick to it. Here we will stick to the one defined above, in particular because my prof used it and so I am passing it on.
However, the reader should be warned that there is a place where the two schools collide: when it comes to theorems relating derivative to monotonicity; therefore when reading about that, one should check what terminology is used.

Important examples
Back to Theory - Introduction