Limit and comparison

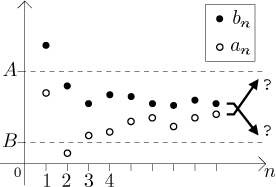
Here we explore the relationship between convergence and comparison by inequality. The main result is the Squeeze theorem.

When two convergent sequences are given, there is a connection between a term-by-term comparison and comparison of their limits:

Theorem.
Let {a_n} be a sequence converging to A and let {b_n} be a sequence converging to B.
(i)    If there is a natural number K such that a_n ≤ b_n for all n > K, then also A ≤ B.
(ii)    If A < B, then there is a natural number K such that a_n < b_n for all n > K.

Both statement should seem obvious when you try to draw some pictures. For the first statement, try to imagine the opposite: that a_n ≤ b_n, yet A > B. If you attempt to draw such a situation, you quickly find that it is not possible. This is not a proof of course, but a good indication.

Similarly, for the second statement you should try to draw a situation when A < B, yet the terms a_n keep jumping to or above b_n now and then.

Note two things. First, it is not possible to make a "sharp" version of the part (i). That is, even if terms of one sequence are sharply greater than the other ones, say, if always a_n < b_n, it is not possible to conclude that A < B, since two different sequences may converge to the same number. For instance, (1/3)ⁿ < (1/2)ⁿ for all natural numbers n, yet both these sequences converge to zero (see geometric sequence in Theory - Limits - Important examples). Thus the best we can say in general is the inequality in the theorem.

Similarly, it is not possible to make the statement in (ii) without sharp inequalities. If we start with the assumption A ≤ B instead of A < B, we would also allow the case of A = B, in which case the terms of the two sequences can well be in any relationship, anything is possible.

Note also that we could have stated the theorem in more generality: We could have allowed the limits A and/or B to be infinite. The theorem would still be true, but we would not really get any extra information. For instance, if we knew that a_n ≤ b_n for all n and that b_n→∞, the theorem would conclude that A ≤ ∞, which is true for all numbers A and therefore not really helpful.

Note that in the theorem we assumed from the start that the two sequences are convergent. This was necessary, it is not possible to derive any conclusion about convergence by comparison. For instance, if we know that one sequence converges to 5 and another is, term-for-term, larger, we cannot say whether this new sequence is convergent as it has too much freedom (by the theorem we just know that if it were, then its limit would have to be at least 5). In order to derive convergence from comparison, one needs much more, see the Squeeze theorem below.

However, sometimes it is possible to force the existence of an improper limit from just one comparison:

The picture should convince you that the first statement is true; the second is equally obvious.

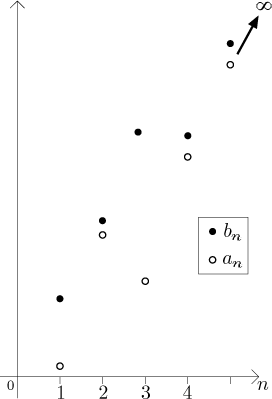
Note that if we have a comparison and one of the sequences goes to infinity, then this situation can be used to draw some conclusion only "half the time", if the comparison goes the right way. How is this meant? Consider for example the situation when for all n we have the comparison a_n ≤ b_n. If we moreover know that a_n→∞, then by this theorem also b_n→∞. If we knew instead that b_n→∞, then we cannot reach any conclusion concerning a_n. This sequence is bounded only from above by a sequence going to infinity, so it has too much freedom left and can go anywhere, even not to have any limit.

We remarked that one bound is not enough to force a convergence. Unlike the above case of improper limit, if we want to force the terms of a given sequence to go to some number, we need two bounds to restrict it from both sides, to prevent the sequence from running away up and down.

Theorem (The Squeeze theorem).
Consider three sequences {a_n}, {b_n}, and {c_n}, such that for all n we have the following:

a_n ≤ b_n ≤ c_n.

If {a_n} converges to some L and {c_n} converges to the same L, then necessarily also {b_n} converges to this L.

Why should such a theorem work? It should seem clear from the following picture:

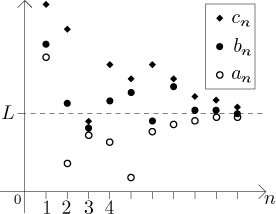
Note that "for all n" actually means "for all n used in indexing the sequences". Since convergence is really determined by the tails of sequences, not their beginnings, it is even enough to assume that the inequalities are true for "n large enough", that is, there is K so that the inequality works for all n > K.

As an application we will prove the folowing result.

Fact.

Proof: We start with the following observation. For all integers n we have

−1 ≤ (−1)ⁿ ≤ 1.

Dividing this inequality by a positive integer n yields

−1/n ≤ (−1)ⁿ/n ≤ 1/n.

Thus we have the given sequence squeezed from both sides, that is, we have an upper and lower estimate. In the language of the Squeeze theorem we would denote

Since −1/n→0 and 1/n→0, by the Squeeze theorem also the given sequence converges to zero as claimed. The proof is complete. The whole procedure may be expressed like this (we make a remark about n being positive, to show why the inequalities did not change their directions when dividing by n).

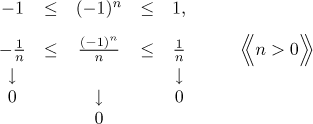
This example was typical. Expressions that oscillate often cause troubles and the usual limit finding methods fail for them, but most oscillating expressions have some natural bound, which just calls for the squeeze to be used.

Note: A proper squeeze has two parts. First, the given sequence must be investigated to find an upper and lower estimate. Second, the upper and lower estimate must converge to the same number. If we had only one estimate, or if the limits of the estimates were not equal, no conclusion about the given sequence is possible. Indeed, note that in the following pictures, the sequence {b_n} may converge to many numbers, it may even be divergent. On the left, we have only a lower estimate for {b_n}, so it can go up any way it pleases; on the right, we have two estimates, but with different limits; again, {b_n} has too much freedom left.

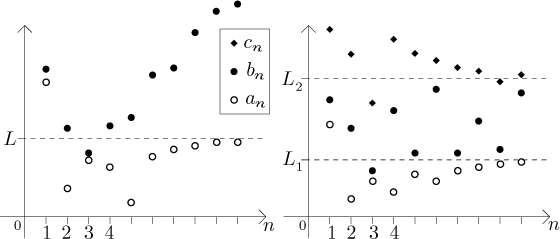
For hints on the proper use of the squeeze we refer to Methods Survey, namely the box "comparison and oscillation".

Sometimes it is more efficient to use absolute value in the squeeze, but it only works for sequences going to zero:

For instance, in the above example we could have argued as follows: For every n we have |(−1)ⁿ| ≤ 1. Consequently also |(−1)ⁿ/n| ≤ 1/n for all positive integers n. Since 1/n converges to zero, also the given sequence must go to zero.

The Squeeze theorem has a nice consequence, a fact that is very useful when calculating limits.

Corollary.
When a bounded sequence is multiplied by a sequence that converges to zero, we get a sequence that converges to zero.
When a bounded sequence is divided by a sequence that converges to infinity, we get a sequence that converges to zero.

In short, "bounded times zero is zero" and "bounded divided by infinity is zero". This is often used.

Sequences and functions
Back to Theory - Limits