Problem: Evaluate the following limit (if it exists)

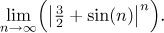
Solution: What happens if we substitute infinity? We get (N + 3/2)^∞ = N^∞. This expression appears in the algebra of DNE as an indeterminate expression; this means that we have to investigate further.

What happens when n goes to infinity? The sine oscillates between −1 and 1, so the whole bracket oscillates between 1/2 and 5/2 (and thus the absolute value is not needed). Since the sine keeps getting almost equal to −1 and 1 again and again all the way to infinity, it follows that 3/2 + sin(n) keeps approaching 1/2 and 5/2 again and again as n grows to infinity. Thus the given sequence has a subsequence that is almost like (1/2)ⁿ and it also has a subsequence that is almost like (5/2)ⁿ. Now recalling the geometric sequence we know that (1/2)ⁿ→0 and (5/2)ⁿ→∞. This would suggest that we have two subsequences, each converging somewhere else, which would mean that the whole given sequence does not have a limit.

But how do we prove it properly? We do not have {(1/2)ⁿ} and {(5/2)ⁿ}, we have "almost (1/2)ⁿ" and "almost (5/2)ⁿ", and we should know by now that "almost" could be quite dangerous when it comes to a limit, especially if the "almost" is raised to a huge power.

Probably the easiest way out is to use arbitrary closedness of sin(n) to −1 and 1 repeated again and again (see Important examples in Theory - Limits). When we chose a small tolerance, the sine will get infinitely many times within this tolerance from −1 and from 1. For instance, we can choose 1/4 as the tolerance. Then there are infinitely many n for which sin(n) < −3/4 and there are infinitely many n for which sin(n) > 3/4.

First, consider the subsequence of natural numbers consisting of n for which sin(n) < −3/4. For this subsequence we also have (sin(n) + 3/2) < 3/4 and therefore

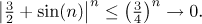
(We only considered n's from this particular subsequence, not all n in this comparison). Thus by the Squeeze theorem, this particular subsequence converges to zero.

Similarly, when we consider the subsequence determined by n for which sin(n) > 3/4, then we also have (sin(n) + 3/2) > 2 and therefore

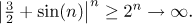
Thus this particular subsequence goes to infinity. Since the given sequence (3/2 + sin(n))ⁿ has two subsequences that tend to different limits, the whole sequence does not have a limit (see Theory - Limits - Basic properties).

Note: To appreciate better the delicateness of the above reasoning, consider the following problem:

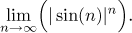
First of all, does it make sense? For a general power to make sense, we must make sure that the base is positive. The absolute value prevents negative numbers from appearing, but what about zero? We know that the sine is equal to zero only at integer multiples of π, but there is only one of them which gives an integer, namely the zero. All other multiples of pi are irrational numbers, so it follows that sin(n) can never be zero if n is a natural number. Good.

So now we know that the sequence makes sense, how about its limit? The numbers |sin(n)| oscillate between 0 and 1, so when we raise them to huge numbers, things start happening. When n is really really huge and |sin(n)| is less than 1 by a lot, then the resulting power is almost zero. For instance, we know that (7/8)^∞ = 0, so all n for which |sin(n)| < 7/8 and which are very large will eventually give very small power. Thus we can make the first observation:

Looking at n for which |sin(n)| < 7/8 we obtain a subsequence that converges to zero. Note that actually most natural numbers are in this subsequence, but there are still infinitely many n that are not there, for which |sin(n)| is closer to 1 then 7/8. So what happens to these "extra" n's? There are two possibilities. One is that also these n, when they get large, make |sin(n)|ⁿ arbitrarily small. Then the whole sequence would tend to zero.

However, it is also possible that these "renegate" n's form a subsequence of {|sin(n)|ⁿ} that does not go to zero, and then, like in the example above, we would conclude that this sequence does not have a limit. Which is the correct alternative?

We may try to include more n in our "zero subsequence" by choosing a smaller tolerance. However, this would not help. For instance, the set of n satisfying |sin(n)| < 11/12 is definitely larger than the one with 7/8 above, but still there are infinitely many n not covered by this subsequence. Similarly, for every q < 1, there is always infinitely many n than make the sine larger than q and so they are not included in the part that goes to zero. This shows that by making the tolerance small we cannot show that the given sequence converges to zero.

What if we try to use those n with large sine to form a second subsequence, the one that has different limit? We would not succeed because we do not have a good lower estimate for them. Indeed, consider the set of n for which, say, |sin(n)| > 7/8. Then we get the comparison

|sin(n)|ⁿ > (7/8)ⁿ→0.

Thus the comparison says that if the subsequence of such n converges, then the resulting limit is 0 or more, which does not help; we needed some estimate that would force the limit to be strictly positive. This shows the difference between the two problems here. In the first problem, we could separate the base from 1 in the right direction. First we found an upper estimate 3/4 for the sine term, and 3/4 is smaller than 1. Since (3/4)^∞ = 0, this estimate forced to given subsequence to zero. In the second example, we could do this, too.

Then, in the first example, we found a lower estimate for the sine base by 2, which is greater than 1, and since 2^∞ = ∞, comparison forced this subsequence to go somewhere else than 0. And that is exactly the difference, in this second problem we cannot find a lower estimate for |sin(n)| by a number greater than 1!

Well, back to the second problem. We have this annoying infinite set of n for which |sin(n)| is almost 1, so we do not know how to force |sin(n)|ⁿ to zero or to some positive number. We know that 1^∞ can be anything, because this is an indefinite power, and unfortunately for us, sin(n) can be as close to 1 even for very large numbers n. However, it is never really equal to 1. sin(n) is always a little bit less than one, and we are raising it to huge numbers. Now recall that those indeterminate expressions are always about the balance of parts. The expression 1^∞ can give zero, assuming that the sequence in the base goes to 1 slower (in some sense) than the sequence in the exponent grows to infinity; loosely, the infinity must be of better quality than the 1 must be 1. So now the question is: Could it be true that every time we take n for which |sin(n)| is very close to 1, then n is already so large that |sin(n)| raised to n gets really small?

In our case, if n was always much bigger (closer to infinity) than |sin(n)| is to 1, then the given sequence converges to zero. How do we decide this? It is not possible with the tools we have at hand. This problem calls for a very thorough and difficult analysis of the sine function. As you can see, the answer to this limit depends on some very arcane knowledge; fortunately, things like this do not happen often.

Back to Solved Problems - Limits