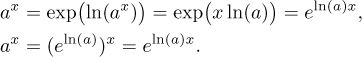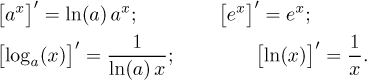Exponentials, logarithms
In the first section we explored
the power AB as a number and then we created the
power function by fixing B and letting A change. Now we will
try it the other way. We fix A and denote it a to emphasize it,
and put x as a variable instead of B. What would be the domain
of a function we thus create? To this end we have to reorganize the
observations from the section on power as a number. There we looked at the
powers from the point of view of B, but now the conclusions have to be
looked at from the point of view of A, that is, a.
If a > 0, then for B we can take any real number. Thus
we have a nice function ax.
If a = 0, we can again take any real number B, in
this way we get the constant function
0x = 1
(including the case 00 = 1). However, this function is
not included in the class we are investigating here since it is very
different. For the same reason we do not include here the case
a = 1, since
1x = 1.
If a < 0, then for B we can only take fractions
whose denominators are odd. However, the set of such numbers (although dense
on the real line) is very scattered and does not contain any interval.
Functions with such domains are pretty much useless from the point of view of
analysis, since most methods require functions defined on non-degenerate
intervals and their unions. Thus we also do not include
a < 0.
In conclusion, we define the general exponential only for
a > 0,
a ≠ 1.
Definition.
By a general exponential function with base
a > 0,
a ≠ 1,
we mean the function ax.
By the exponential function we mean the function
ex, where e is the Euler number
2.718281828...
Sometimes we also write exp(x) or
Exp(x) instead of
ex, especially if the argument is a more complicated
expression.
The number e has to be defined somehow. The most common definition is
using a limit, the Euler number is defined as the limit of the
sequence (1 + 1/n)n,
see Sequences - Theory -
Important examples.
The general exponential function has real numbers as the domain. The
algebraic properties of powers translate to some useful properties of the
general exponential function, for all real x,y, and
c we have
ax + y =
ax⋅ay;
ac⋅x =
(ax)c =
(ac)x
The general exponential is monotone, namely increasing for
a > 1 and
decreasing for a between 0 and 1. In both cases the general
exponential is concave up. There is a natural ordering between the general
exponential functions. The inequality
a < b implies
ax < bx
for x positive and
bx > ax
for x negative.
The graphs are like this:
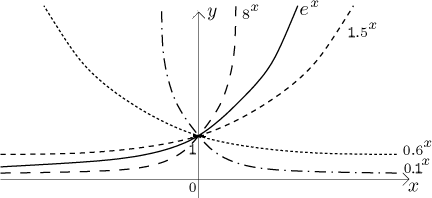
We see that the range is
R(ax) = (0,∞). If a > 1, then

For a∈(0,1) we
have

Logarithm
For a > 0, a ≠ 1, the general exponential
ax is a monotone
function on its domain and therefore 1-1. Thus it has an inverse. This
inverse is called the logarithm with base a and denoted
loga(x). That is, for a positive x, the
loga(x) is such a number y that
a y = x.
The special case, when a = e,
is called the natural
logarithm and is denoted ln(x). In engineering, the logarithm with
base a = 10 is often used, it is called the decadic
logarithm and usually denoted log(x).
The properties of logarithm naturally follow from properties of the general
exponential. There are two important algebraic identities:
loga(x⋅y)
= loga(x) + loga(y);
loga(xc)
= c⋅loga(x).
By the way, although many students get very creative during tests, there is
really no identity for
loga(x + y).
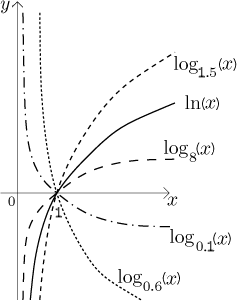
The domain of a logarithm is (0,∞), the range is the whole real line and
loga(1) = 0. Logarithm is monotone -- increasing for
a > 1, decreasing for a∈(0,1) -- and concave down. Important limits at endpoints
are for a > 1:

and for
a∈(0,1):

This follows easily from the graphs:
Again, there is a natural ordering, but this time it is more complicated and
depends on comparing the base to 1. If
a < b < 1 or
1 < a < b, then
loga(x) < logb(x)
for x∈(0,1)
and
logb(x) < loga(x)
for x > 1.
If a < 1 < b, then
logb(x) < loga(x)
for x∈(0,1)
and
loga(x) < logb(x)
for x > 1.
The fact that a logarithm is the inverse to the appropriate general
exponential can be expressed by these important equalities:
x = loga(ax)
for x real and
x = aloga(x)
for x > 0.
When applied to the natural logarithm, these equalities say that
x = ln(ex) for real x and
x = eln(x) for positive x. The latter
equality is very useful, here in Math Tutor we call it the "e to ln trick".
In particuar, using it one can deduce the following identities which show
that it is in fact enough to know the exponential (with the base
e) and the natural logarithm, since for every
a > 0 we have

Indeed, the second equality requires just a little thought and the first
equality is even easier, we will show it two ways:
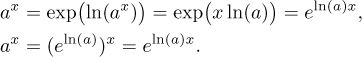
We conclude this section with formulas for derivatives:
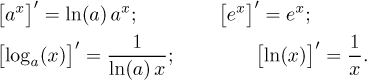
Interesting remark: There are several ways in which to define the
exponential. Mathematicians like abstract things and so they often use this
version:
Exponential is the function f defined on a real line that
satisfies f (0) = 1,
f ′(0) = 1, and
f (x + y) = f (x)⋅f (y)
for all x,y.
Of course, one has to prove that there is only one such function, but this
can be done, and since our exponential has these properties, it must be the
one. Similarly one can define the general exponential by changing the second
condition to f ′(0)=ln(a).
General powers
Back to Theory - Elementary
functions


![]()
![]()
![]()
![]()

![]()