Here we will not consider asymptoticity as a theoretical comparison of functions around points (see Order of functions and asymptotes in Functions - Theory - Real functions). Rather, for the purpose of graph sketching we will understand asymptote as a straight line that has the property that some "end" of the graph follows this straight line. This calls for a different definition; in fact we have two or three kinds of asymptotes (depending how we count them).
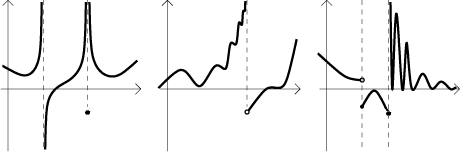
Vertical asymptotes. Before we give a formal definition, we look at this picture:

The first two pictures on the left show vertical asymptotes, the vertical lines in the last picture on the right are not asymptotes (the situation on the right of that picture is that the function keeps oscillating up and down as it approaches that point, the size of oscillation going to infinity, for a similar example see Example 3 in "saw-like" functions in Functions - Theory - Elementary functions). This should suggest the right definition.
Definition.
We say that a function f has a vertical asymptote at a (or that the linex = a is a vertical asymptote of f ) if at least one one-sided limit of f at a is improper.
This definition also tells us how to find such an asymptote. First we have to collect all candidates. From the definition it is clear that if f is continuous at a, then it cannot have a vertical asymptote there. What points are left? Proper endpoints of intervals composing the domain and the points inside these intervals where f is not (or may not be) continuous. For each of these points we look at all possible one-sided limits and if at least one is improper, we get a vertical asymptote there.
As usual, nothing bad happens if we include extra points in our list of candidates, we simply rule them out in the next step. This is the reason why in "real life" we do not really bother actually identifying points of discontinuity, we simply include among candidates all points where the continuity is for some reason suspect. One-sided limits then decide asymptotes, note that if we wanted to really know continuity at such points, we would have to calculate the one-sided limits anyway, so we save work by not worrying about continuity. We can save more work if at a given point the first one-sided limit we check is improper, since then we already have an asymptote and there is no reason to evaluate the other (if there is any).
Horizontal asymptotes. Before we give a formal definition, we look at this picture:
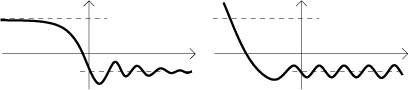
The first picture shows horizontal asymptotes, the horizontal lines in the second picture are not asymptotes. This should suggest the right definition.
Definition.
Let a function f be defined on a neighborhood of infinity. We say that the liney = a is a horizontal asymptote of f at infinity if the limit of f at infinity is a.
Let a function f be defined on a neighborhood of negative infinity. We say that the liney = a is a horizontal asymptote of f at negative infinity if the limit of f at negative infinity is a.
This definition tells us right away how to find such asymptotes.
Oblique asymptotes. Before we give a formal definition, we look at this picture:
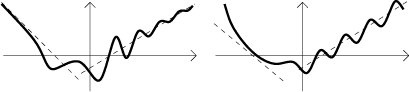
The first picture shows oblique asymptotes, the lines in the second picture are not asymptotes.
Definition.
Let a function f be defined on a neighborhood of infinity. We say that the liney = Ax + B is an oblique asymptote of f at infinity if
Let a function f be defined on a neighborhood of negative infinity. We say that the line
y = Ax + B is an oblique asymptote of f at negative infinity if
How do we find such asymptotes?
Fact.
Let a function f be defined on a neighborhood of infinity. The liney = Ax + B is an oblique asymptote of f at infinity if and only if
Analogous statement is true for asymptote at negative infinity. We see that in order to get a line, the constants A and B must exist, in other words, the two limits should converge. If they do, we have the asymptote. Note also that to evaluate the second limit we have to know the outcome of the first limit. This suggests a general procedure for identifying oblique asymptotes.
We start with the first limit. If it diverges, there is no asymptote at
infinity. If it converges, we can try the second limit. If it diverges, there
is no asymptote at infinity. If it converges, we have the asymptote
Remark: Note that the procedure described above also yields horizontal
asymptotes. Indeed, if f has limit b at infinity, then the
procedure first gives
There are some good reasons. The horizontal asymptote differs in two important aspects. First, finding it is much easier than finding non-horizontal oblique asymptotes, we just interpret a limit at (negative) infinity. Second, when a function has a horizontal asymptote at infinity, its behavior is much different compared to functions that have non-horizontal oblique asymptotes at infinity. Still, some authors do not see these reasons as sufficient to split one notion into two, they just work with vertical and oblique asymptotes.
Here in Math Tutor we do take horizontal asymptotes as a special case, which allows us to refine the algorithm for oblique asymptotes further. We always start with the limit at infinity (for negative infinity we have obvious modifications). If the limit does not exist, then there is no asymptote at infinity. If it is proper, then we have a horizontal asymptote there. If it is improper, we have a chance for an oblique asymptote.
Then we try the limit to get A. If it diverges, then there is no
oblique asymptote. However, now also the result
We refer to Asymptotes in Methods Survey - Graphing for a practical overview.
Example: Find all asymptotes of
![]()
Solution:
The domain is
![]()
We got an improper one-sided limit, so it is not necessary to look at the
second one. We know that f has a vertical asymptote at
Now we look at infinity:
![]()
Thus there is no horizontal asymptote, but we may have an oblique one. We try to get A:
![]()
At infinity we do not have an oblique asymptote either.
Now we look at negative infinity:
![]()
There is a horizontal asymptote