In this section we explore the connection between the Riemann and Newton integrals. Note that these two integrals are very different in nature. To start with, the Riemann integral is a definite integral, therefore it yields a number, whereas the Newton integral yields a set of functions (antiderivatives). The Riemann integral is a geometric notion (area), while the Newton integral is an algebraic notion. Finally, these integrals apply to different sets of functions. As we will see, both can be applied to "nice" functions; on the other hand, for instance the jump function we saw before is Riemann integrable, but it does not have an antiderivative.
It may therefore come as a surprise that in fact, there is a deep connection between these two. This is the topic of this section. As one of the consequences we will find a convenient way of evaluating definite integrals.
We start with a definition. Let f be a function that is Riemann
integrable on an interval
![]()
Note that since we used x as an upper limit, we cannot use it as a
variable in the integral and had to choose another letter. The value of

Since we can define this number F(x) for all x from [a,b], we obtained a function on [a,b] in this way. For a possible interpretation of this integral, click here. We have the following:
Theorem (The Fundamental Theorem of Calculus I, TFC 1).
Let f be a function that is Riemann integrable on[a,b], let c belong to[a,b]. For x from[a,b], define
Then F is a continuous function on
[a,b]. Moreover, for x from(a,b), if f is continuous at x, then F is differentiable at x andF ′(x) = f (x).
Example: Consider the function
Let c=1. If
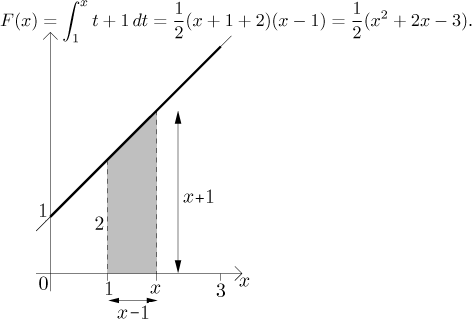
If
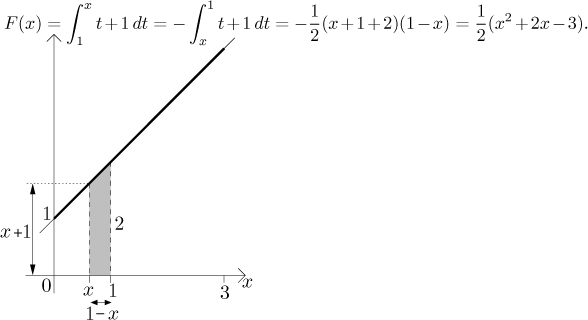
Thus on
![]()
Indeed, we now see that F is continuous on
Since most of the time we deal with continuous functions and these are Riemann integrable, we have this weaker but useful version:
Theorem (The Fundamental Theorem of Calculus I, TFC 1).
Let f be a continuous function on[a,b], let c belong to[a,b]. For x from[a,b] we define
Then F is an antiderivative of f on
[a,b].
We now have the first connection. We see that a continuous function is both Riemann integrable and Newton integrable, and we can get an antiderivative (the Newton integral) using the Riemann integral. There is a connection the other way, too:
Theorem (The Fundamental Theorem of Calculus II, TFC 2).
Let f be a continuous function on[a,b]. If F is an antiderivative of f on[a,b], then
This is also called the Newton-Leibniz Formula. Since finding an antiderivative is usually easier than working with partitions, this will be our preferred way of evaluating Riemann integrals. Since this is used so often, in calculations we will be also using this convenient notation:
![]()
Example: We know that
![]()
Recall that when we find a Newton integral, we express it as
![]()
The Newton-Leibniz formula can be also used in case when
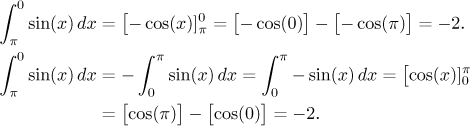
The two Fundamental Theorems show that for a continuous function, the Riemann and Newton integrals are somehow connected. A more general statement is also true.
That strange integral at the beginning did not just come out of the blue, in fact it has a natural interpretation in physics. The Fundamental theorem then follows from elementary physical reasoning, it is a very useful take on this topic and we offer it in this note. Here we will show a useful mathematical interpretation.
Recall that given a function, if we first integrate it and then diffferentiate, we arrive at the same function as in the beginning. However, if we first differentiate and then integrate, then this no longer works (see Newton integral in Integrals - Theory - Introduction). However, when we look at our results here not from the point of view of f, but we focus on F, we get a very interesting formula:
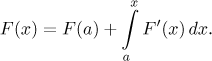
So if we differentiate a function, we can recover it by integrating it if we use the definite integral in the right way.