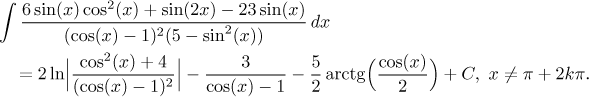Příklad: Vypočítejte integrál
![]()
Řešení: Tento integrál zapadá do šuplíku goniometrické integrály, ale ne k nějakému specifickému typu. Je to velice blízké typu poslednímu, racionální (lomené) funkce se siny a kosiny, ale tam zase vadí ten dvojnásobek v sinu nahoře. Toho se ale snadno zbavíme, vypadá to pak takto.
![]()
Teď už je to jen integrál se siny a kosiny. Víme, že nás pak univerzální substituce určitě dokáže zbavit goniometrických funkcí, ale víme také, že to je nouzové řešení, kterému je lepší se vyhnout, zde to dopadne takto. Většinou se ovšem snažíme o nějakou lepší variantu, ideálně sinovou a kosinovou substituci. Šlo by to zde? Na sinovou substituci potřebujeme u dx kosinus a nezdá se, že bychom je tam uměli nějak rozumně vyrobit.
Na kosinovou substituci potřebujeme u dx sinus a ten tam snadno vytkneme z čitatele, čili kosinová substituce by určitě šla, teď je ovšem třeba zajistit, aby to, co v integrálu po vytknutí kosinu zbude, byly jen siny. Z tohoto pohledu vadí ten sinus ve jmenovateli, ale naštěstí je tam ve druhé mocnině, takže jej bezbolestně převedeme na kosinus.
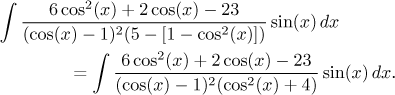
Povedlo se, jsme zralí na substituci.
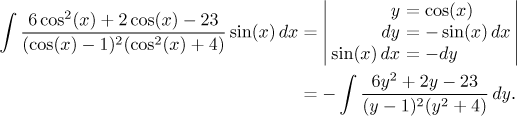
Toto je klasický integrál z racionální (lomené) funkce, postupujeme tedy příslušným algoritmem. Nejprve ověříme, že je stupeň čitatele menší než stupeň jmenovatele, to platí. Pak bychom měli co nejvíce rozložit jmenovatel, to už se také stalo. Je tedy načase udělat rozklad na parciální zlomky. Budou tři se čtyřmi neznámými konstantami. Jednu konstantu získáme snadno zakrývací metodou, ostatní dostaneme ze tří rovnic, které obdržíme například násobící metodou, která zde dá trochu víc práce. Zajímavou alternativou je proto kombinace limitní a dosazovací metody. Oba přístupy ukážeme zde, čtenář se vydá cestou, kterou má nejraději. Dostáváme
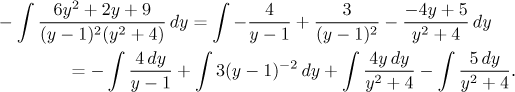
Kvadratický zlomek jsme rozdělili na dvě části, protože tak máme integrovat kvadratické parciální zlomky, naštěstí jsme předtím nemuseli doplňovat čtverec ve jmenovateli. Teď budeme integrovat. První dva integrály jsou elementární, třetí se řeší kvadratickou substitucí. Pro ten poslední standardní algoritmus doporučuje nepřímou substituci.
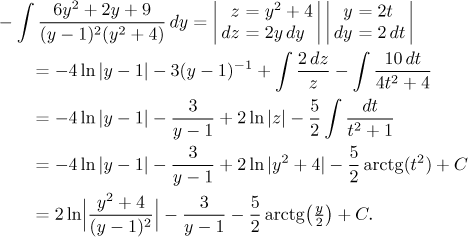
Zbývá udělat zpětnou substituci. Jaká bude podmínka platnosti? Vidíme, že y nesmí být 1, tedy kosinus nesmí být 1.