Jde o integrály typu
![]() ,
kde p a q jsou polynomy. Máme pro ně standardní postup.
,
kde p a q jsou polynomy. Máme pro ně standardní postup.
Algoritmus pro integrování podílu polynomů.
Krok 1. Pokud není stupeň čitatele menší než stupeň jmenovatele,
vydělte (pomocí algoritmu na
dělení polynomů)
čitatel jmenovatelem se zbytkem. Dále se budeme věnovat jen zbytku,
což je podíl polynomů, který již má stupeň čitatele menší než stupeň
jmenovatele.
Krok 2. Rozložte jmenovatel, co to jde, tedy na součin mocnin
lineárních faktorů a mocnin ireducibilních (dále nerozložitelných)
kvadratických faktorů.
Krok 3. Rozložte podíl polynomů na součet parciálních zlomků.
Krok 4. Integrujte ty parciální zlomky.
Než se na ty kroky podíváme blíže, tak poznamenáme, že se vyplatí nejprve ověřit, jestli čitatel náhodou není roven (až na násobek) derivaci jmenovatele. V tom případě by totiž čel integrál snadno vyřešit pomocí substituce a nebyla by třeba ona dlouhá procedura výše.
Krok 2 je úloha z oboru lineární algebry. Často je již jmenovatel rozložený, někdy stačí něco vytknout, jindy je třeba hledat kořeny, což se nejčastěji dělá pomocí kvadratického vzorce či (u polynomů vyššího stupně) odhadem. Detailnější povídání se najde v sekci Polynomy v části Funkce - Teorie - Elementární funkce. O tom, jak lze uhádnout rozklad kvadratického polynomu, je tato poznámka.
Krok 3 je vlastně samostatné téma a vyhradili jsme mu samostatnou stránku.
Krok 4: Vidíme, že abychom dokázali integrovat racionální funkce, stačí nám umět integrovat následující dva typy integrálů:
![]()
Pro oba máme standardní postup.
Parciální zlomky s lineárními členy: Tyto se snadno integrují pomocí
zjevné lineární substituce. Pro
![]()
Pro
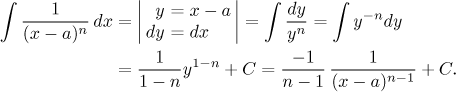
Příklady, kde v
Parciální zlomky s kvadratickými členy: Tyto mohou být snadné až delší, podle toho, jak je člen komplikovaný. Začneme tím nejjednodušším a ukážeme, jak se komplikovanější situace převádějí na ty základní. Obecně je strategie taková, že pokud je v čitateli x, tak se využije ke kvadratické substituci, což je ten snažší případ. Pokud je v čitateli konstanta, pak se integrály převádí směrem k integrálu arkus tangensovému.
a) Základní typ s konstantou v čitateli se snadno převede na tabulkový integrál jednoduchou nepřímou substitucí.
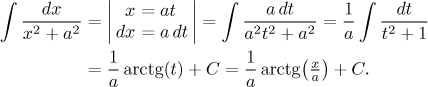
Někteří lidé si tento integrál pamatují. Transformace se dá dělat i dalším způsobem, nejprve vytknout a ze jmenovatele a pak použít přímou substituci, viz zde.
b) Základní typ s x v čitateli se snadno řeší pomocí kvadratické substituce.
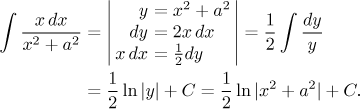
Člen, která má v čitateli jak x tak konstantu, se snadno rozdělí na dva integrály, které již umíme řešit.
![]()
Teď si přidáme komplikace, začneme vyšší mocninou ve jmenovateli.
c) Člen s x v čitateli není problém, protože kvadratická
substituce pořád funguje. Pro
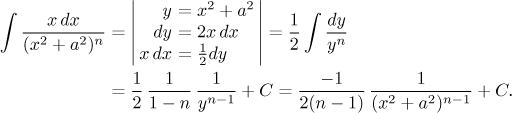
d) Člen s konstantou v čitateli a vyšší mocninou ve jmenovateli je ze všech nejhorší, protože se nedá přímo spočítat. Namísto toho se používá redukční vzorec, kterým v každém snižujeme mocninu o jedničku, dokud se nedostaneme k integrálu vedoucímu na arkus tangens. Redukční vzorec:
![]()
Pokud vás zajímá, odkud se vzala, klikněte
sem.
Existuje alternativa, zacházet s tímto integrálem podle návodu v šuplíku
"mocniny kvadrátu", což může být
snažší pro
e) Zbývá probrat nejobecnější případ, když máme ve jmenovateli obecný kvadratický výraz. Zde postup volá po doplnění čtverce ve jmenovateli, substituce pak daný integrál převede na typy, které už umíme řešit.
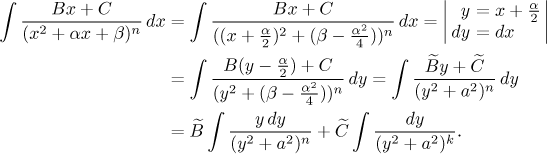
Dá se ušetřit čas tím, že se tento postup zkombinuje se substitucí z a),
výsledná smíšená substituce
Všimněte si, jak záleží na pořadí, je nutné se nejprve zbavit lineární části ve jmenovateli a teprve potom se čitatel rozdělí na dva zlomky. Pokud bychom pořadí změnili a nejprve rozdělili integrál na dva, jeden s x a druhý s konstantou v čitateli, pak by se ten integrál s x po substituci změnil v integrál, který má v čitateli jak y tak konstantu, čímž bychom byli nuceni jej znovu zbytečně rozdělovat. Existuje alternativní algoritmus, který se tomuto problému vyhýbá, některým čtenářům by mohl přijít pohodlnější a popisujeme jej zde. Zde v Math Tutoru se nicméně budeme držet postupu popsanému výše.
Poznamenejme také, že po doplnění na čtverec vždy dostáváme výraz
Uvedený postup lze mírně modifikovat, aby lépe pasoval na konkrétní situaci. Pár modifikací si ukážeme v následujícím příkladě.
Příklad: Začneme s výpočtem následujícího integrálu. Protože stupeň čitatele není menší než stupeň jmenovatele, začneme dělením se zbytkem a pak se zaměříme na ten zbytek. Dalším krokem je rozložení jmenovatele na faktory, pak napíšeme rozklad na parciální zlomky.
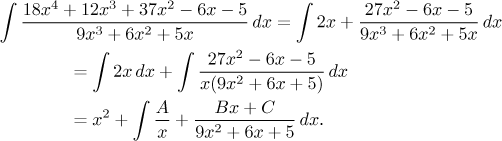
Všimněte si, že nepostupujeme úplně přesně podle teoretického rozkladu. Správně bychom totiž měli vytknout devítku z kvadratického jmenovatele, aby začínal členem x2. Vznikly by ale zbytečně zlomky, takže se jim (alespoň zatím) vyhneme. Dá se ukázat, že se tím nic nezkazí, jen budeme muset modifikovat jeden z dalších kroků.
Neznámé konstanty získáme relativně snadno, protože jsou jen tři. Máme jeden reálný kořen, takže jednu konstantu získáme zdarma pomocí "zakrývací" metody, ostatní dvě dostaneme například násobící metodou.
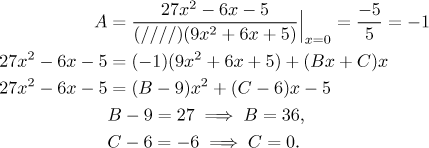
Dostáváme tedy
![]()
První parciální zlomek je lineární a proto velice snadný, soustředíme se proto na druhý, který padne do případu e). Nejprve máme doplnit čtverec. Všimněte si, že nás přitom nebude trápit konstanta 9, kterou jsme nevytkli, prostě ji do doplnění zahrneme. Pak použijeme doporučovanou smíšenou substituci, která odstraní lineární část a rovnou vyrobí ve jmenovateli 1.
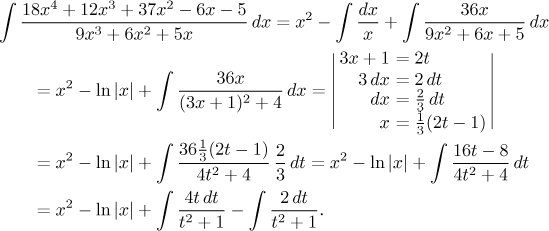
Teď už snadno dokončíme výpočet.
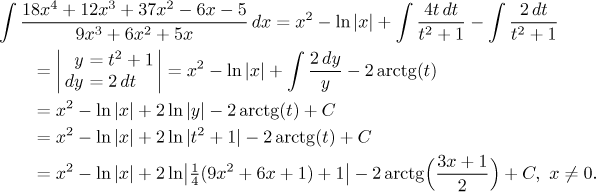
Zbývá upravit výsledek. Pomocí indentity pro logaritmus součinu oddělíme tu
čtvrtinu pryč jako samostnatný člen
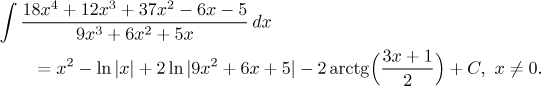
Většina příkladů v části Řešené příklady - Integrace vede nakonec na parciální zlomky, takže máte dostatek ukázek, obzvláště zajímavý je tento příklad, tento příklad, tento příklad a tento příklad.
Další šuplík: integrály s odmocninami
Zpět na Přehled metod -
Metody integrace