Šuplík "neurčitý součin"

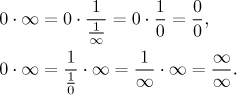
Zde se podíváme na následující problém: Potřebujeme najít limitu součinu f⋅g v nějakém a a poté, co jsme zkusili dosadit a, jsme dostali neurčitý součin 0⋅∞.

Standardní řešení je převést algebraicky součin na podíl. Pokud to uděláme tak, jak je ukázáno níže, pak tento podíl bude neurčitého typu a můžeme aplikovat triky ze šuplíku "neurčitý podíl", nejspíše l'Hospitalovo pravidlo.

Jak změníme součin ve zlomek? Zvolíme jeden ze členů v součinu a aplikujeme trik "jedna děleno jednou dělenou"; víme totiž z algebry, že pro libovolné nenulové A máme A = 1/(1/A). Výsledný podíl bude typu, který závisí na tom, jakou část součinu jsme takto přeměnili, zda tu "nulovou" nebo tu "nekonečnou":

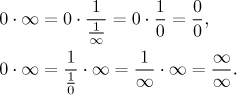
Všimněte si, že v druhé variantě jsme vlastně podváděli, když jsme napsali 1/0 = ∞. Víme, že když dělíme nulou, musíme zkontrolovat její typ, jen pak můžeme dojít k nějakému závěru. Protože nevíme, zda "0" v součinu je opravdu jednostranná, musíme zde být trochu opatrní. Pokud je, pak dostaneme plus nebo mínus nekonečno, jak jsme ukázali výše. A když ta nula není jednostranná? Pokud plánujeme následně použít l'Hospitalovo pravidlo, tak to není problém, protože jeho obecná verze vyžaduje, aby absolutní hodnota jmenovatele šla k nekonečnu, a platí 1/|0| = ∞

Většinou ale problémy nemáme.

Příklad:

Máme neurčitý součin, proto jej zkusíme změnit v podíl. Se kterou částí si budeme hrát? Musíme vzít v úvahu dvě věci. Za prvé, část, se kterou si budeme hrát, se změní, bude tam navíc složení s mocninou na −1, takže obvykle zvolíme ke hraní tu část, která se příliš nezmění (z pohledu derivace) po přidání mocniny na −1. Druhý (a obvykle méně důležitý) faktor je tento: Bylo by pěkné, kdyby se ta část, se kterou nebudeme nic dělat, po zderivování zlepšila.

V tomto příkladu je tedy volba jasná. Budeme si hrát s částí x, protože x⁻¹ je vlastně stejný druh výrazu, jmenovitě mocnina, takže derivováním zase dostaneme něco jednoduchého, mocninu. Část, kterou necháme být, ten logaritmus, je zase nahrazen po derivaci další mocninou, což je pěkný bonus.

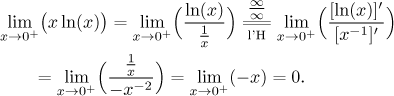
Co se stane, když si zkusíme hrát s druhou částí součinu? Protože [ln(x)]⁻¹ je znatelně horší než ln(x) z pohledu derivace, můžem čekat problémy.

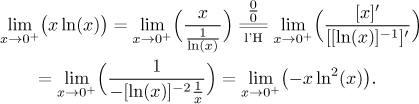
Jak vidíte, nový výraz je ještě horší než s čím jsme začali, takže takhle to nepůjde. To naznačuje, že naše volba převodu na podíl rozhodne, zda uspějeme nebo ne.

V části Řešené příklady - Limita jsou tyto metody použity v tomto příkladě a tomto příkladě.

Další šuplík: neurčitý rozdíl
Zpět na Přehled metod - Limita