Theorem (Comparison test, CT).
Consider series
• If
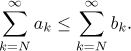
• If
In the previous section we tried to compare series to geometric series. There is another kind of a series that we understand well, namely p-series (series with powers). When we are given a series, we may ask whether it is similar to some p-series; more generally, we try to compare it to another series that we know well. The main trick used in such comparison is that we try to ignore parts that are less important for large k (see e.g. Intuitive evaluation in Sequences - Theory - Limit).
If we want to show that the behavior of a given series is just like that of another (probably simpler) series (we will call it a test series), we have two possibilities. One is direct comparison.
Theorem (Comparison test, CT).
Consider series∑ ak and∑ bk such that0 ≤ ak ≤ bk for all k.
• If∑ bk converges, then also∑ ak converges and
• If
∑ ak diverges, then also∑ bk diverges.
The idea of this theorem is very simple: If we have some inequality true between terms of the series, then the same inequality is also true for the series; it is as if we added all those individual inequalities, which is something that we can safely do for finitely many inequalities. This theorem shows that we can also do it for infinitely many inequalities on condition that the numbers involved are positive (or zero) and that we are resigned to the fact that sometimes we do not get any conclusion.
Indeed, imagine that we try to do this:
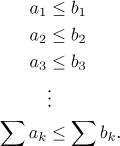
What meaning does the last line have? The theorem above shows that common sense provides correct answers. First, assume that the series on the left diverges. Then its sum is infinity (by this theorem, its terms are positive or zero) and the sum on the right is larger, so it must also be infinity. Thus we obtained the second statement above.
If the series on the left converges, then the sum is a real number. The sum on the right is larger, but this can mean a larger (or equal) real number but also infinity. Thus common sense suggests that the series on the right has too much freedom. Indeed, the theorem above does not provide any conclusion for this situation.
Now assume that the series on the right converges. Then its sum is a real number and the sum on the left is smaller (or equal), so it also must be a real number and we get convergence. (This is a tricky part, how do we know that the series does not start oscillating in the space afforded to it by the upper bound? Here the positivity of terms comes to the rescue, without it this comparison would fail.)
Finally, if the series on the right diverges, then its sum is infinity (positive terms again) and the sum on the left is less or equal. Thus it can be a real number or infinity, we have no way to know and no conclusion is possible.
We just saw that there are good reasons why the two statements in the theorem are just implications, not equivalences. This is in fact the greatest drawback of this test. If we establish inequality between two series and get information about one of them, then there is only a 50 percent chance that this conclusion can be passed on to the other series. One more remark: If at least one inequality between the individual terms is sharp, then also the inequality between the two sums is sharp. (Which does not alter the substance of test, we know that one can have sharp inequality also between two infinities.)
Example: Investigate the convergence of
![]() .
.
We apply the Comparison test. First we have to find a good test series. Usually the best way to find one is to ask what parts of ak are not important for large k. In this case we know that we can ignore the "+13". In this way we get the test series and we can proceed by trying to find some comparison between the given series and the test series (both have positive terms, so there is no problem with Comparison test).
![]()
Since the series on the right is known to converge (the p-test, see Important examples in Theory - Introduction), and it is larger, then also the given series must converge.
Example: Investigate the convergence of
![]() .
.
We apply the Comparison test. We already saw above the most natural candidate for the test series, so we try it.
![]()
The series on the left converges, but the one on the right is greater, so it might be a number but also infinity. This time the Comparison test gave no conclusion.
Remark: We just saw the best and the worst of the Comparison test. If it works, then it is usually very simple to get conclusions. However, it is very sensitive to small changes and easily fails to yield any answer.
Actually, this last example is so simple that with a bit of work it can be handled by the Comparison test. There are two possible strategies. If we think that the given series diverges, then we may attempt to somehow make our test series larger so that it diverges, but still smaller than the given series in order to push it to infinity. On the other hand, if we think that the given series converges, then instead of going for a lower estimate we would need an upper estimate by a series that converges to force it down.
Experience suggests that the expression
2k2 − 13 > k2.
Thus we can estimate as follows:
![]()
Since the series on the right converges, the given series also converges by Comparison test.
We just saw that with a bit of imagination, even the less reliable Comparison test can be made to work. Still, often it is simpler to use the other comparison test coming up right now.
The direct comparison above used inequality. Sometimes we may also use another kind of comparison, when we say that for large k two things are about the same. This has the advantage that such a situation is naturally symmetric, so statements will go both ways. Disadvantage is that "being about the same" is a tricky statement that has to be somehow made precise and substantiated in concrete cases, which means more work.
Theorem (Limit comparison test, LCT).
Consider series∑ ak and∑ bk such thatak > 0 andbk > 0 for all k.
Assume that
converges and
A > 0.
Then∑ ak converges if and only if∑ bk converges.
In other words,
Why do we have the limit assumption there? In a typical case, if the test
series is chosen carefully, we get
![]()
Now if the series on the right is convergent, then its sum is a number, this
is multiplied by A to give another number (here we use that A is
not infinity) and it follows that also the series on the left should add up
to a number. If the series on the right is divergent, then the sum is
infinity and A times infinity is infinity (assuming that
Similarly we argue that information passes from left to right, again the cases when A is zero or infinity turn out to be bad, so we see why the assumption of the theorem rules these two cases out.
Example: Investigate the convergence of
![]() .
.
We know
that when k is large, then the terms of this series look
like
So we use the Limit comparison test. We claim that when k is large,
then the given terms are about the same as
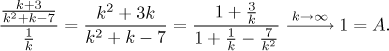
We confirmed that our guess was correct, so the given series behaves the same as the test series, that is, the harmonic series. Since that series diverges, by the Limit comparison test also the given series diverges.
Symbolically,
![]()
Note: Again, an experienced series investigator could find a way to use comparison here, for instance by claiming that for large k one has
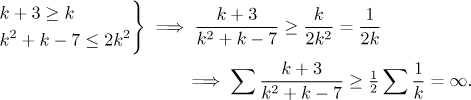
However, establishing the second inequality above is best done using a limit, so one may as well go to Limit comparison.
The Comparison test and the Limit comparison test have in general different requirements on the test series. When we are given a series and want to use comparison for it, then we look for terms bk that are always greater (or always smaller) than the given ak. Thus these two terms need not be really similar, the difference can be quite large. On the other hand, if we plan on using the limit comparison, then we need the test series to have bk pretty much the same as the given ak but we do not care about their mutual position. This suggests that it would not be quite correct to claim that one test is more powerful than the other, and indeed there are series for which one test works and the other does not. However, in practice also the ordinary comparison works best if bk are similar to ak, otherwise the test series becomes too different and we often end up with the situation that no conclusion is possible. For instance, if we want to show by comparison that a given series is convergent, then we need an upper estimate, but if we go up by too much, then the test series becomes divergent (sums up to infinity) and we fail. Thus it pays off to choose the test series as close as possible to the given one.
There are other tests that use comparison, but they are not covered in standard calculus courses. As an example we will show this one.
Theorem.
Consider series∑ ak and∑ bk such thatak > 0 andbk > 0 for all k. Assume that there is an integer N such that for allk > N we have
• If
∑ bk converges, then also∑ ak converges.
• If∑ ak diverges, then also∑ bk diverges.
For more information see Methods Survey - Comparison tests and Solved Problems - Testing convergence, namely this problem, this problem, this problem, this problem, this problem, and this problem.